Raul Fattore
April 7, 2023
The present study is divided into six parts
Part-1 Part-2 Part-3 Part-4 Part-6
Table of Contents
In This Paper
Following the analysis made in Part-3, the third remaining external force is evaluated in this study.
The nuclear response to external forces is analyzed with the aim to observe any changes in the nuclear mass and study the behavior of the refractive index under such changes.
The analysis will be performed in the time domain as well as in the frequency domain by means of the Fast Fourier Transform (FFT) method. The external forces applied to the nucleus were classified into three types:
- The force originated by a polarized transverse electromagnetic wave (TEM) (see Part-3)
- The force originated by a polarized TEM plus a static electric field (see Part-4)
- The force originated from a signal plus a static electric field
Abstract
Some efforts have been made to prove negative mass behavior through some experiments performed in mechanics [1], and other disciplines [9], as well as some theories in electrostatics [2,3,4,5,6,7,8], but I haven’t found research about similar effects at the atomic level, where the most elementary mass given by the atomic nucleus is to be found.
- Is the second Newton’s law still valid with negative mass?
- What could happen if we make the atom behave in a negative mass regime?
- Is the negative refractive index related to negative mass?
- Are we able to control the magnitude of mass?
- Are we able to control the sign of mass?
The answers to these questions are given through this series of papers, with results that are coincident with experimental data, except for the negative mass regime. Experiments must be done to confirm or invalidate the theory developed in these articles. Needless to say, if experiments validate this theory, then a significant change in mankind is going to happen. In that case, I strongly ask scientists to cooperate by making use of the derived technologies for good and refrain from doing it for evil.
Introduction
The theory presented in these papers, as described in Part-1, is based on three fundamental aspects that have proved to be extremely effective to describe physical phenomena and predicting results that agree with experimental data [10, 11, 12]:
• Spinning Ring Model of Elementary Particles (toroidal ring of continuous charge)
• New Atomic Model
• The Universal Electrodynamic Force
Based on the new atomic model, a shell arrangement of the nuclear particles has been assumed in Part 1, as shown in Fig. 1.
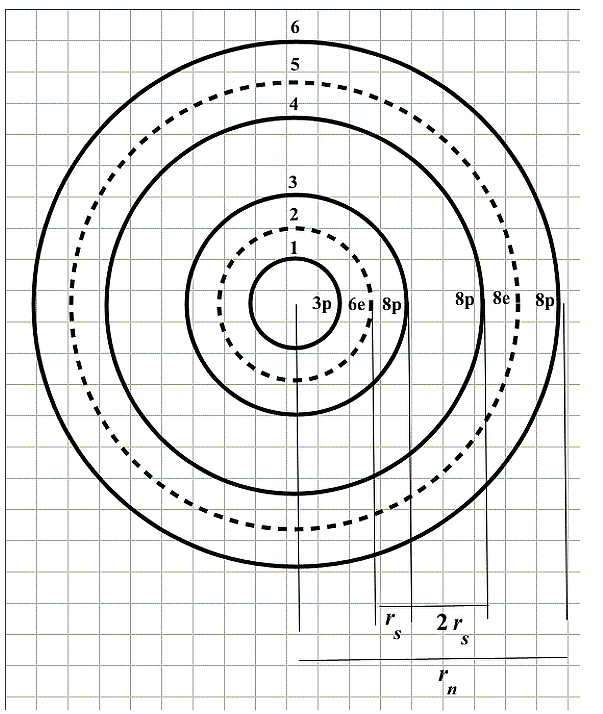
Assumed shell arrangement for Aluminum atomic nucleus
This sandwich configuration keeps the particles very tightly bound together. Note that at three shells in from the outermost shell, there are always two proton shells in a row for the larger nuclides.
This weak binding allows the outermost sandwich of shells to have liquid-like properties and forms the proper justification for a Liquid Drop Model of the nucleus.
As we already know, the torus ring model of the particles has an associated electric field as well as a magnetic field. However, due to the very tight packing configuration of the particles, we may safely assume that the distance among shells is extremely tiny and that the predominant force in the nucleus is of electrostatic origin, while the weaker magnetic forces will add some contribution to the equilibrium distance between each shell. As demonstrated in Part 1, mass is an intrinsic property of the atomic nucleus. Under natural circumstances, it has a constant universal magnitude and is always positive. However, with some proper external agents, we might be able to manipulate the intrinsic mass by changing its magnitude and sign.
III. Nuclear Response to Force Caused by an Electric Signal plus a Static Electric Field
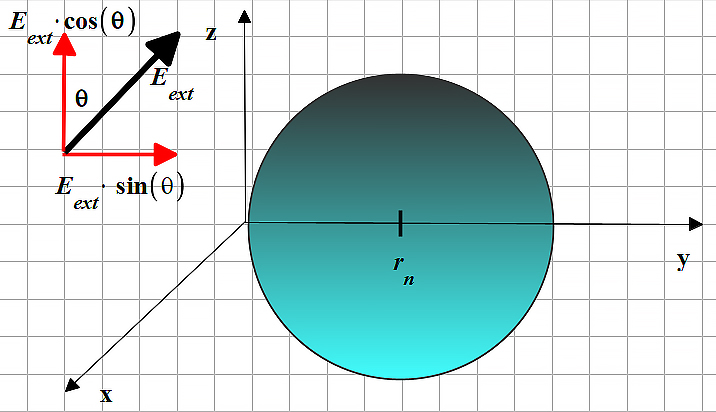
External signal and static electric field acting on the nucleus
Let’s take an external excitation composed of a uniform electric field ![]() plus a signal with amplitude
plus a signal with amplitude ![]() and frequency
and frequency ![]() , which is overlaid with the static field.
, which is overlaid with the static field.
Assume also that the composed field is given as in Fig. 2 by ![]() , where
, where ![]() is the magnitude of the static electric field.
is the magnitude of the static electric field.
Assume that the external field ![]() is parallel to the z-y plane, making an angle
is parallel to the z-y plane, making an angle ![]() with the z-axis.
with the z-axis.
The components of the field in cartesian coordinates are: ![]() , and in spherical coordinates we have,
, and in spherical coordinates we have,
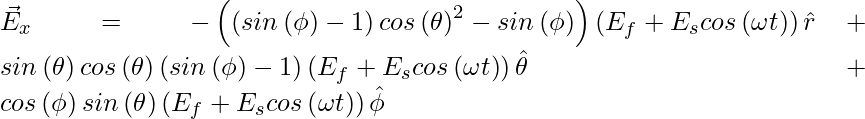 (1)
(1)
Consider that the effect of the force caused by this external field is distributed in the entire nucleus volume. Then, a reasonable approach will be to average the external field over the nuclear volume, that is,
![]()
![]()
The result of this integral gives us the averaged field in the nucleus,
![]() (2)
(2)
The electric field ![]() gives the direction of the external force. The total force exerted by the field on the nucleus is the sum of the forces on every proton and electron, which form the nuclear shells. According to our 6 shells structure (Fig. 1), we have:
gives the direction of the external force. The total force exerted by the field on the nucleus is the sum of the forces on every proton and electron, which form the nuclear shells. According to our 6 shells structure (Fig. 1), we have:
![]() , where
, where ![]() is the total nuclear charge. Based on the shell structure of Fig. 1 and taking the sign of the charges for each shell, we get
is the total nuclear charge. Based on the shell structure of Fig. 1 and taking the sign of the charges for each shell, we get
![]() (3)
(3)
By replacing Eq. (2) in (3), we obtain the (rough) final expression of the external force acting on the nucleus:
![]() (4)
(4)
Now that we have the external force exerted on the nucleus caused by an electric signal plus a static electric field, let’s evaluate the nuclear response related to mass and refractive index behaviors.
III.a Nuclear Mass Analysis due to a Force caused by a Static Electric Field plus an Electric Signal – Partial or Total Energy Absorption
The intrinsic net force in the nucleus was already defined with Eq. (23) in Part-1. Now we have the action of an external force acting on the nucleus that will interact with the internal force. By applying Newton’s second law, we have
![]() =>
=> ![]()
![]() (7)
(7)
By replacing the forces in (7), we obtain the expression of the nuclear mass for this case:
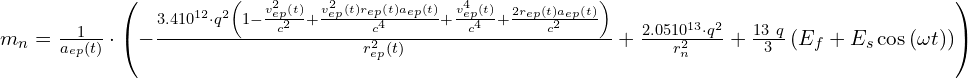 (8)
(8)
Recall that:
![]()
![]()
![]()
Some graphs as examples are shown below to have a perception of what could be done to modify the nuclear mass magnitude and sign.
The main parameters used for the net force are:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]()
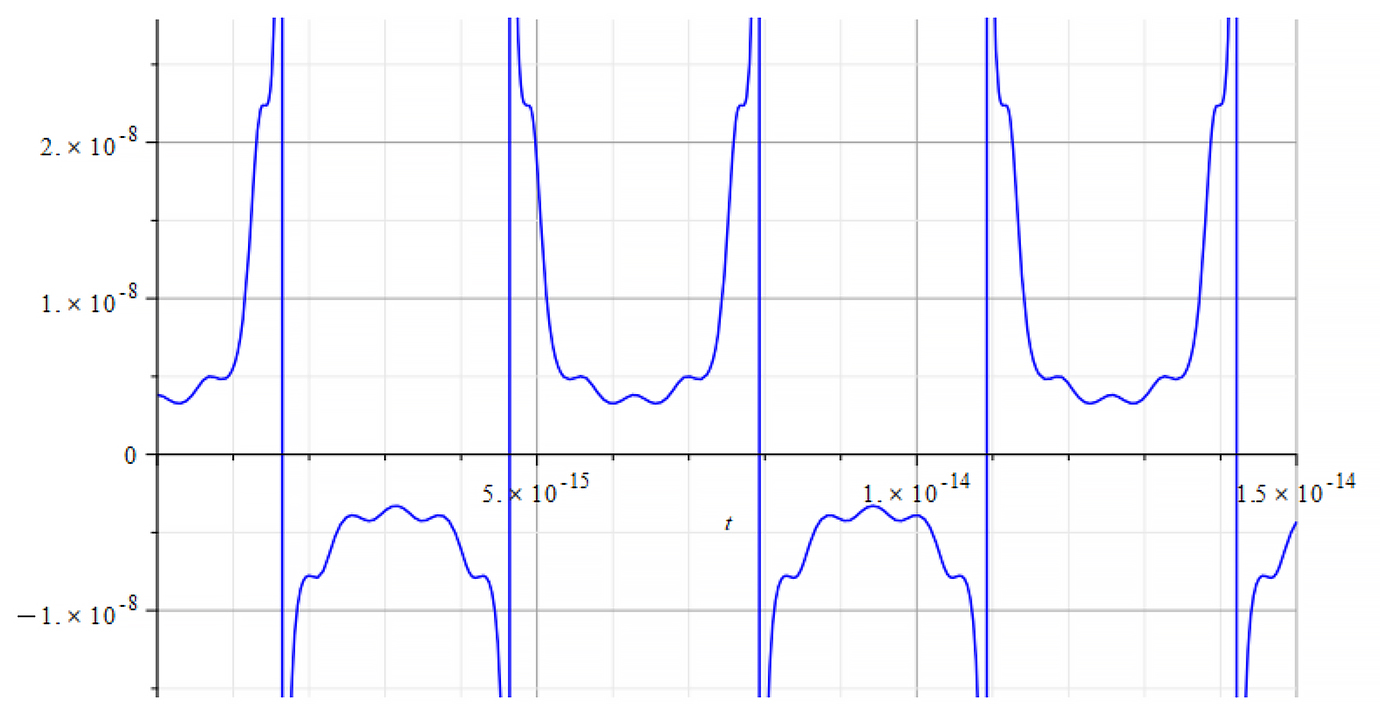
Time Analysis of the Nuclear Mass
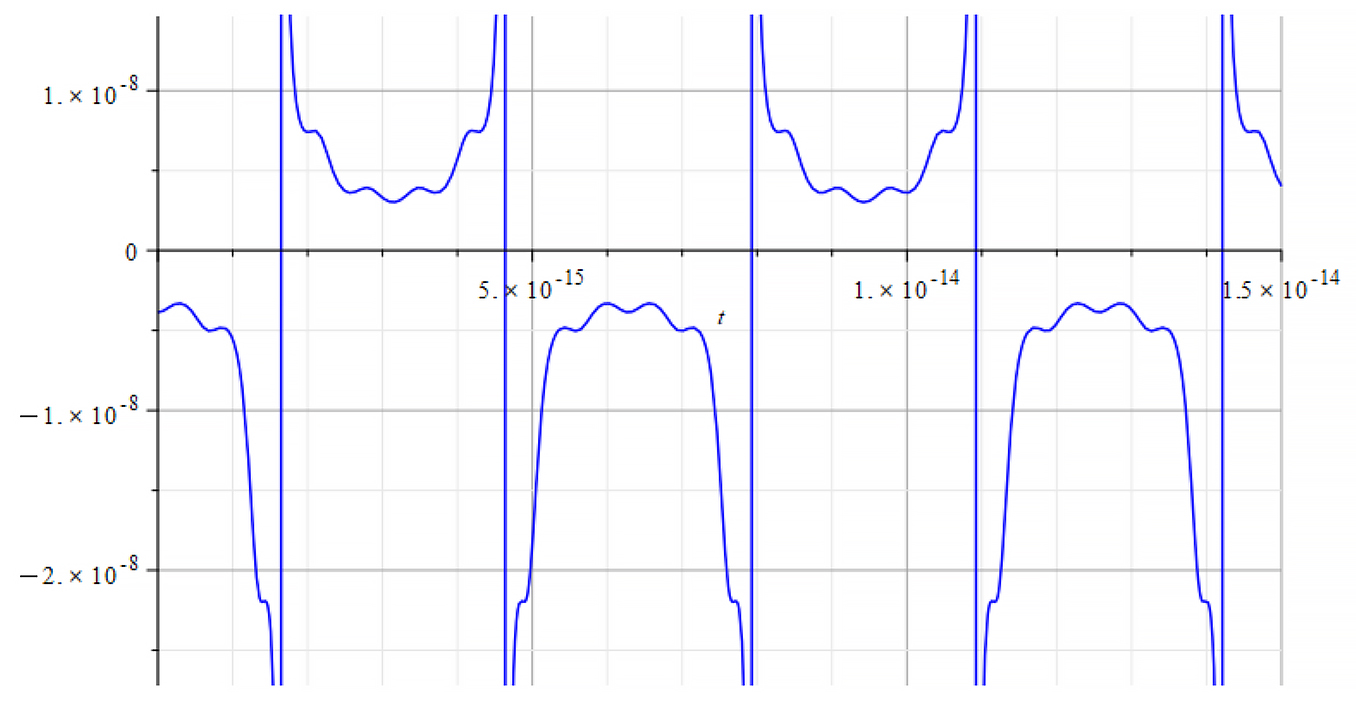 |  |
Mass vs. time for the following parameters: | Mass vs. time for the following parameters: |
 |  |
Mass vs. time for the following parameters: | Mass vs. time for the following parameters: |
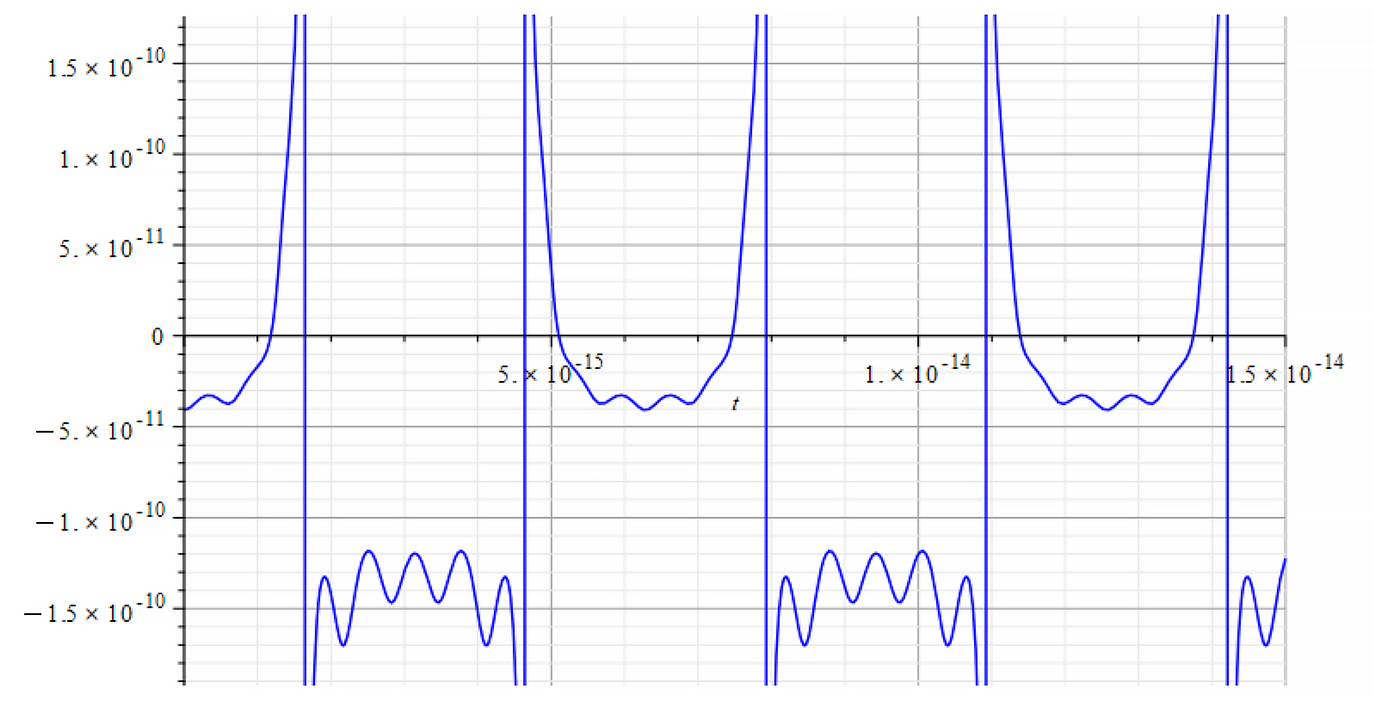 | 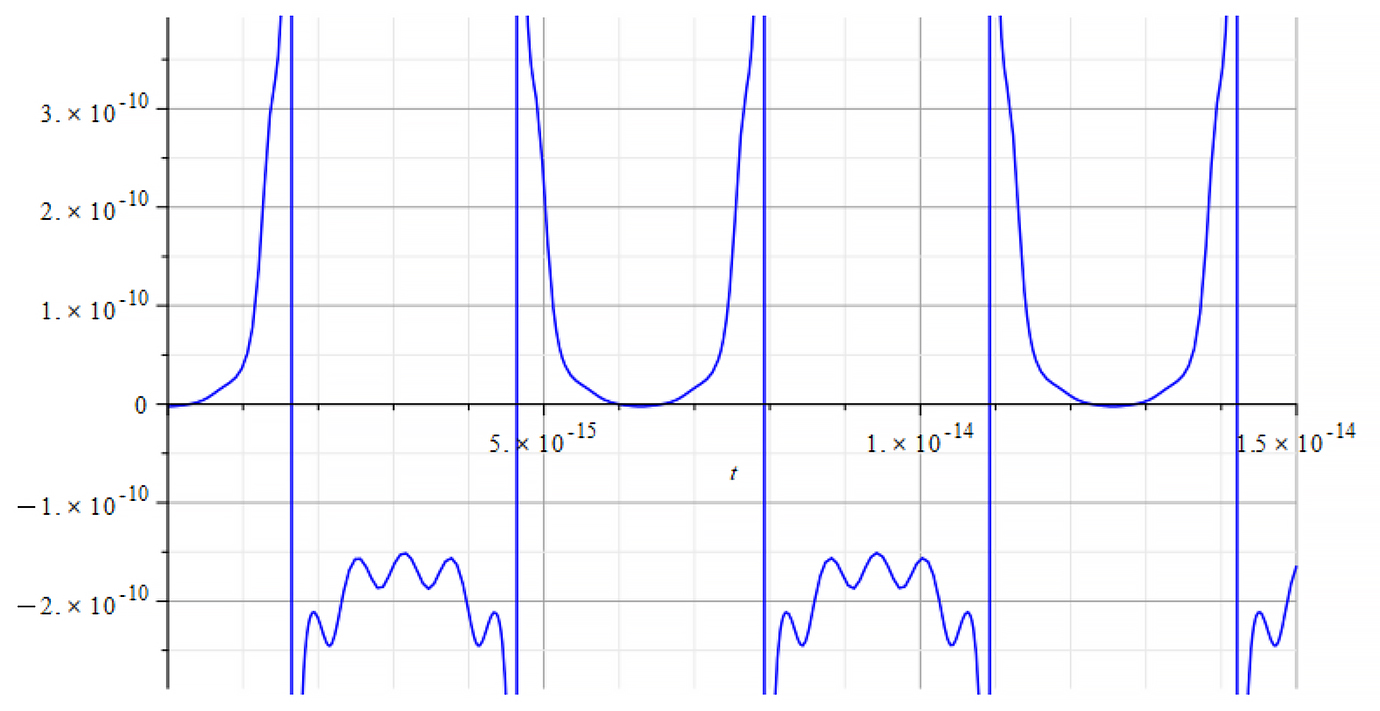 |
Mass vs. time for the following parameters: | Mass vs. time for the following parameters: |
From the period of the mass plot, we determine that the oscillation frequency is approximately:
![]()
Frequency Analysis of the Nuclear Mass with FFT
Total number of samples ![]() , sampling frequency
, sampling frequency ![]() (proton frequency), which gives a frequency resolution
(proton frequency), which gives a frequency resolution ![]() and a total acquisition time of
and a total acquisition time of ![]() . The frequency at the i-sample number on the plot is determined by
. The frequency at the i-sample number on the plot is determined by ![]() .
.
For +Ef
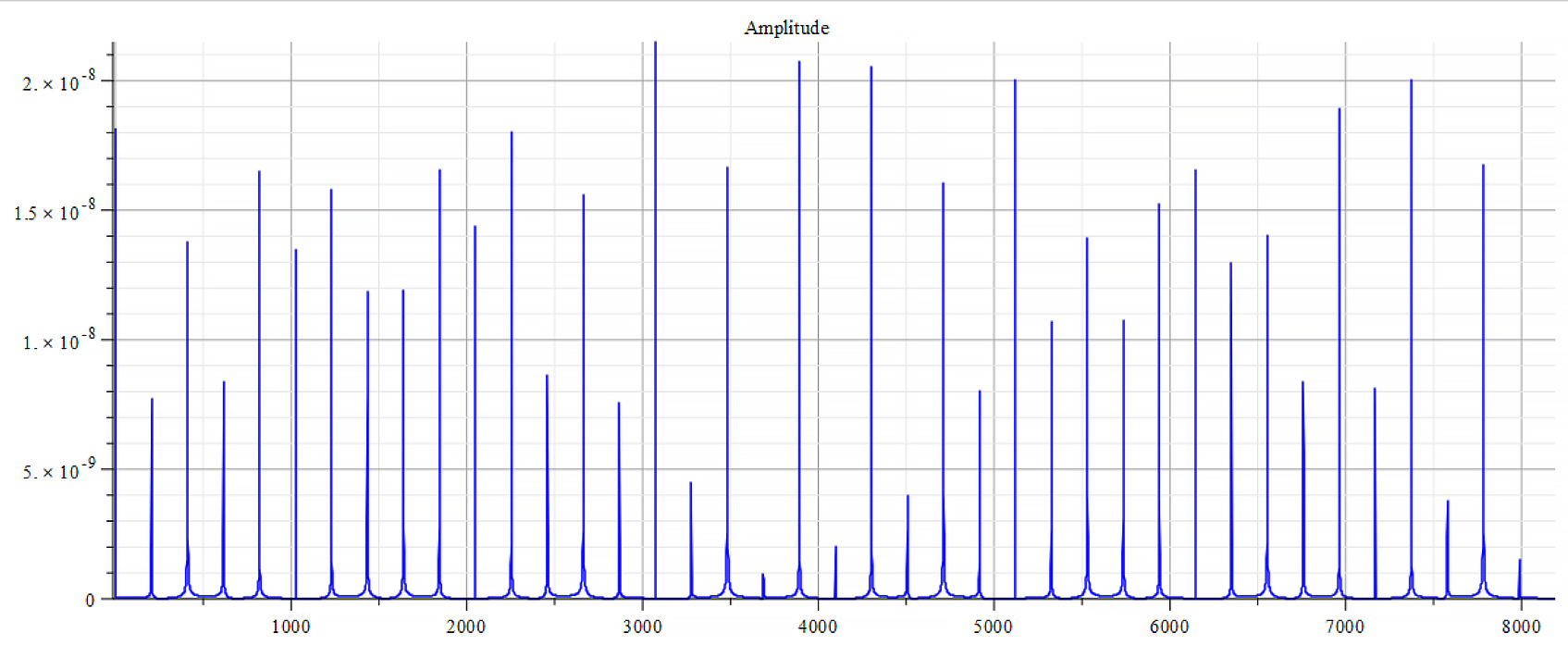
Frequency spectrum for the following parameters:
![Rendered by QuickLaTeX.com \omega={10}^{15}\ [\frac{1}{s}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-40e9be72c982500305e076b28d6e9710_l3.png) ;
;![Rendered by QuickLaTeX.com E_s={10}^{18}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-c9758917948eb87857658b1f0ac3c81c_l3.png) ;
; ![Rendered by QuickLaTeX.com E_f={10}^{24}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-0be8419b03b5c46f5e1200b68a49789b_l3.png)
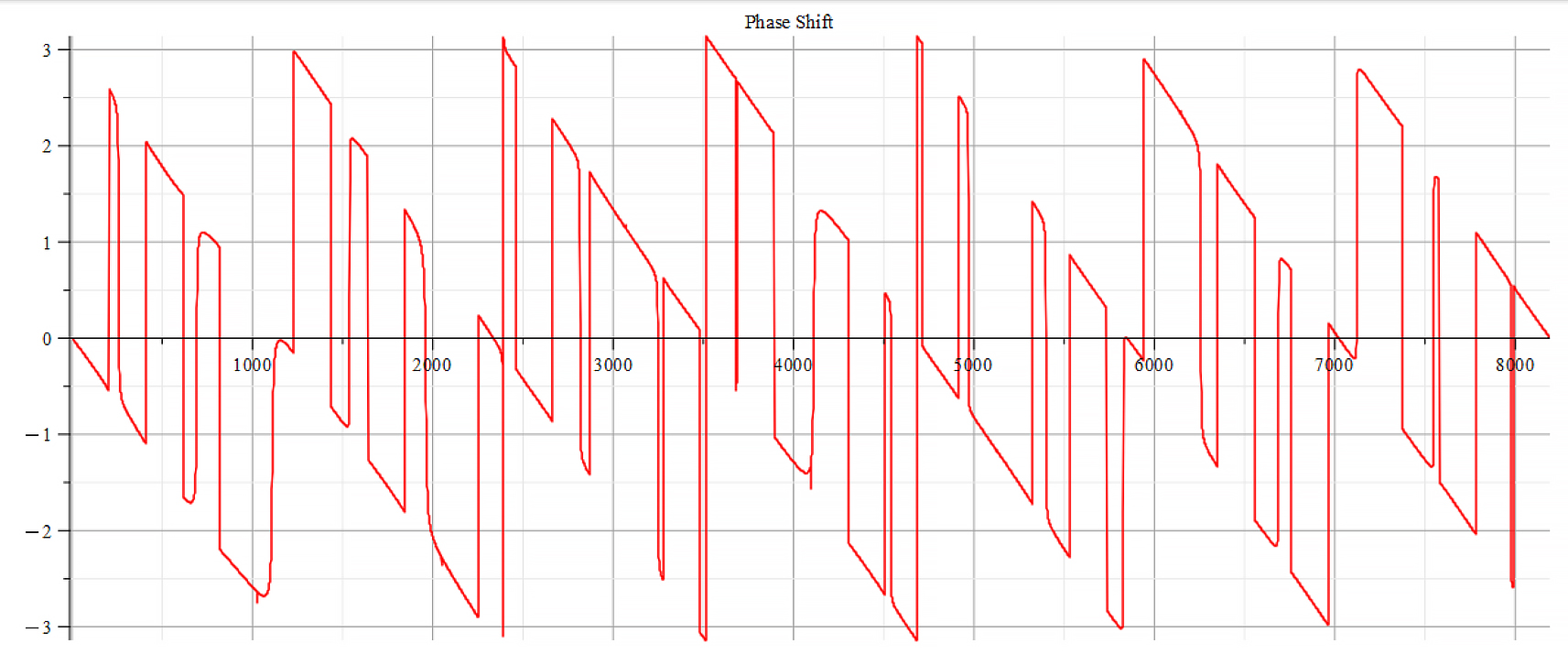
Phase shift for the following parameters:
![Rendered by QuickLaTeX.com \omega={10}^{15}\ [\frac{1}{s}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-40e9be72c982500305e076b28d6e9710_l3.png) ;
; ![Rendered by QuickLaTeX.com E_s={10}^{18}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-c9758917948eb87857658b1f0ac3c81c_l3.png) ;
; ![Rendered by QuickLaTeX.com E_f={10}^{24}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-0be8419b03b5c46f5e1200b68a49789b_l3.png)
For -Ef
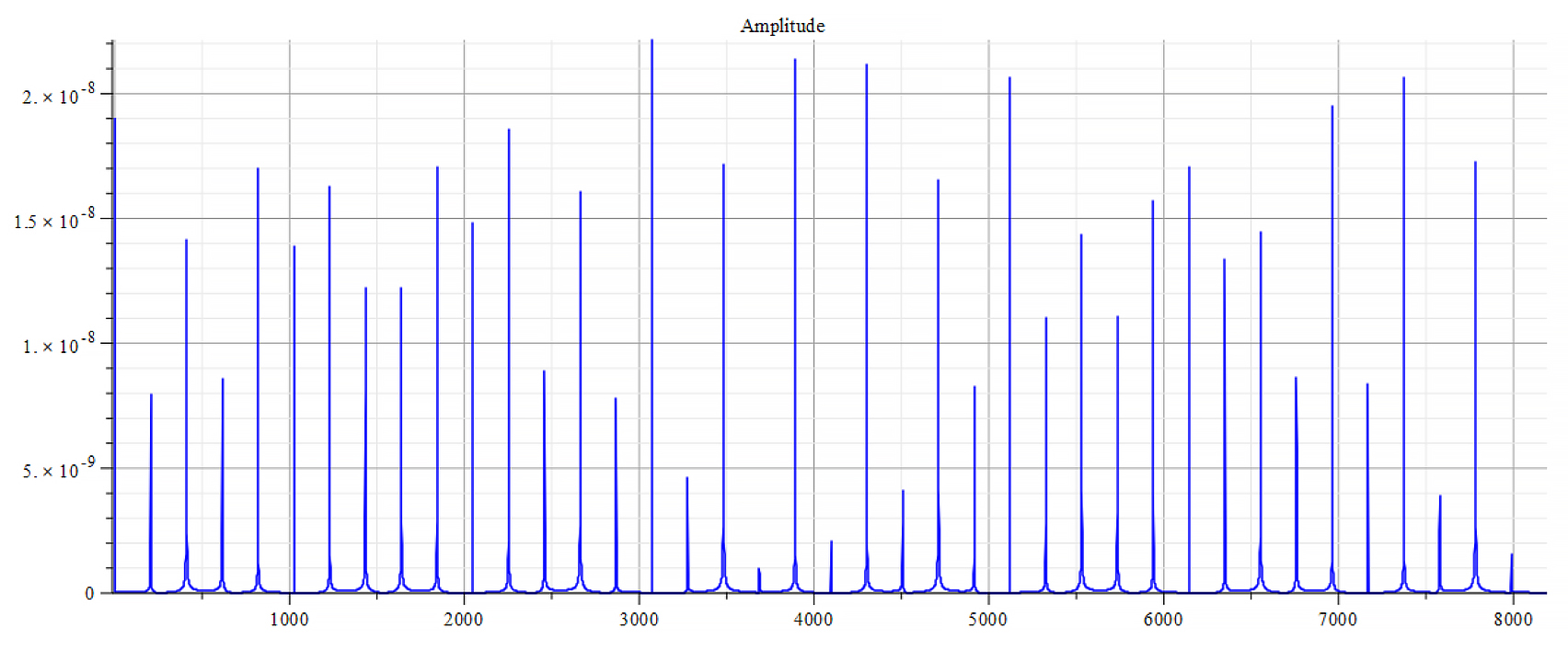
Frequency spectrum for the following parameters:
![Rendered by QuickLaTeX.com \omega={10}^{15}\ [\frac{1}{s}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-40e9be72c982500305e076b28d6e9710_l3.png) ;
; ![Rendered by QuickLaTeX.com E_s={10}^{18}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-c9758917948eb87857658b1f0ac3c81c_l3.png) ;
; ![Rendered by QuickLaTeX.com E_f={-10}^{24}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-88f64fa36345871e50058f89d0f0b821_l3.png)
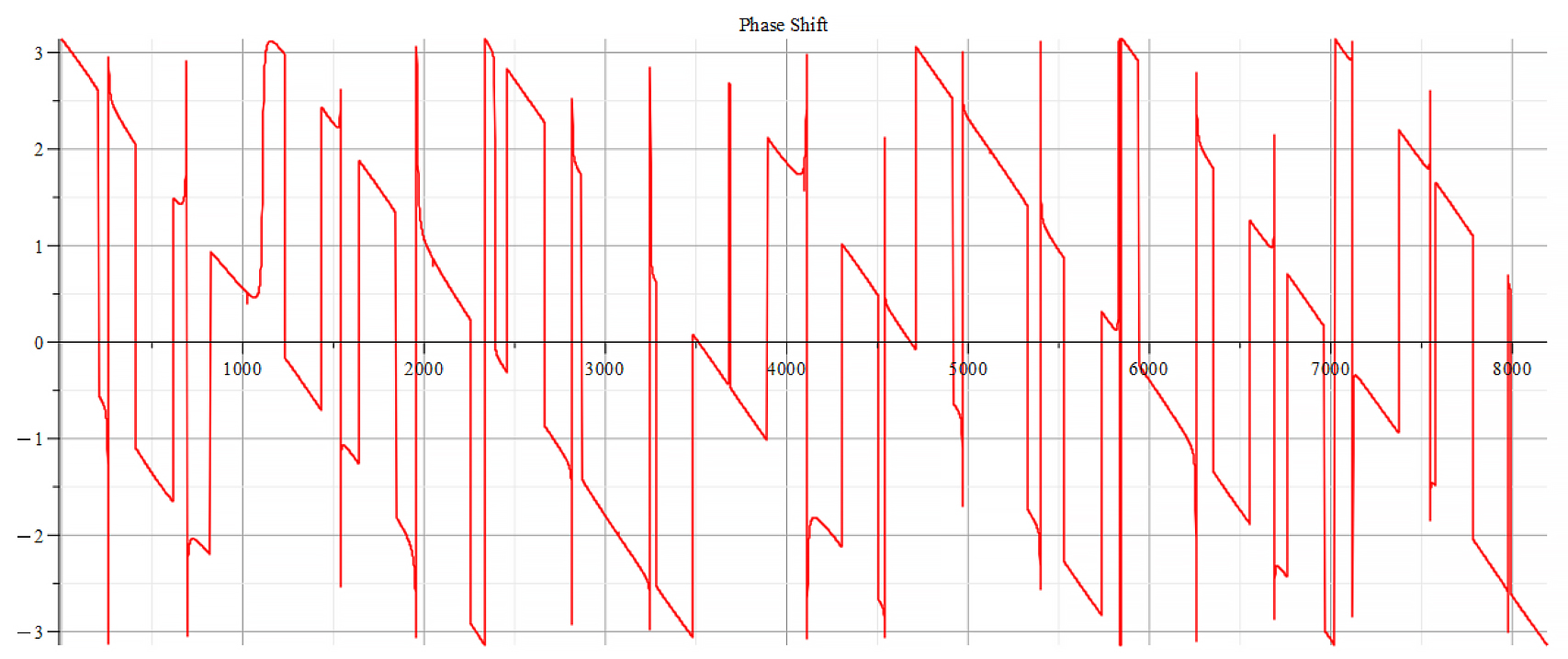
Phase shift for the following parameters:
![Rendered by QuickLaTeX.com \omega={10}^{15}\ [\frac{1}{s}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-40e9be72c982500305e076b28d6e9710_l3.png) ;
; ![Rendered by QuickLaTeX.com E_s={10}^{18}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-c9758917948eb87857658b1f0ac3c81c_l3.png) ;
; ![Rendered by QuickLaTeX.com E_f={-10}^{24}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-88f64fa36345871e50058f89d0f0b821_l3.png)
For +Ef
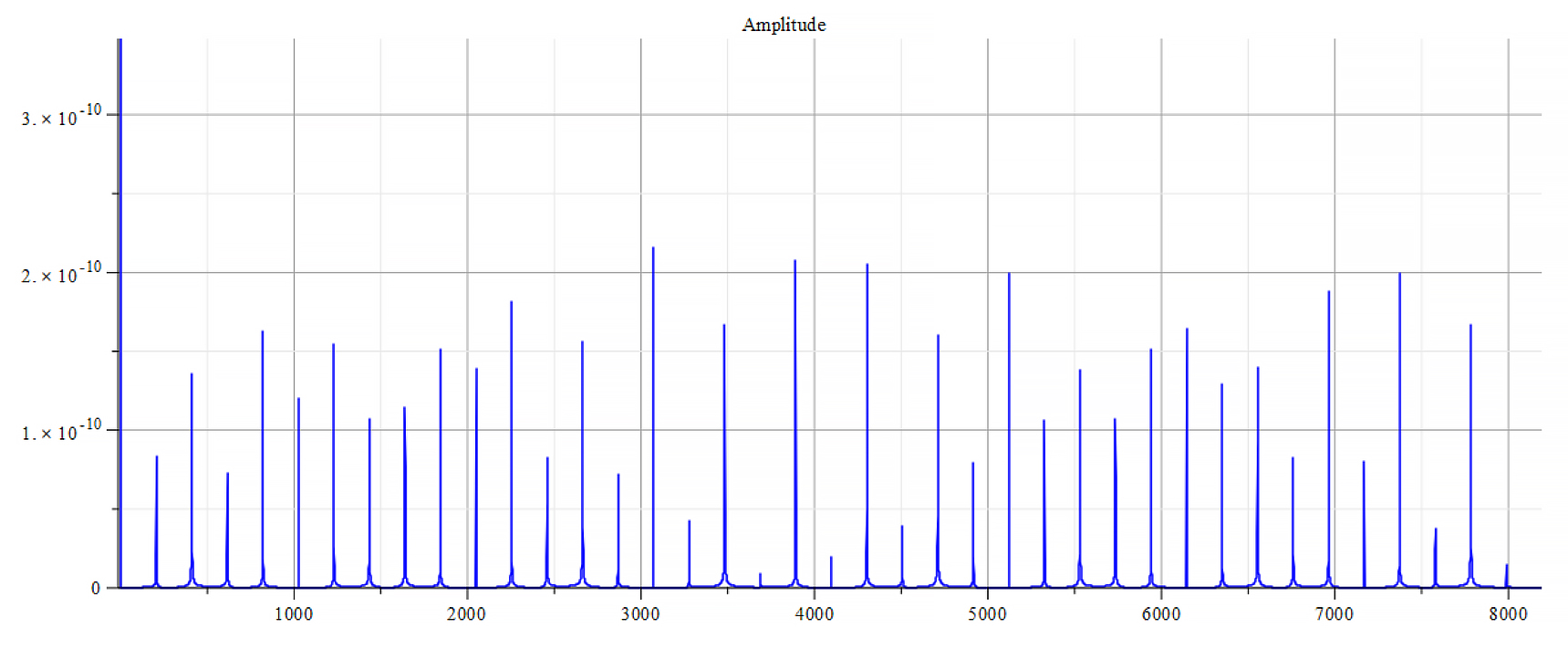
Frequency spectrum for the following parameters:
![Rendered by QuickLaTeX.com \omega={10}^{15}\ [\frac{1}{s}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-40e9be72c982500305e076b28d6e9710_l3.png) ;
; ![Rendered by QuickLaTeX.com E_s={10}^{18}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-c9758917948eb87857658b1f0ac3c81c_l3.png) ;
; ![Rendered by QuickLaTeX.com E_f={5\ 10}^{21}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-26b9acb5d123063310834690dff0970a_l3.png)
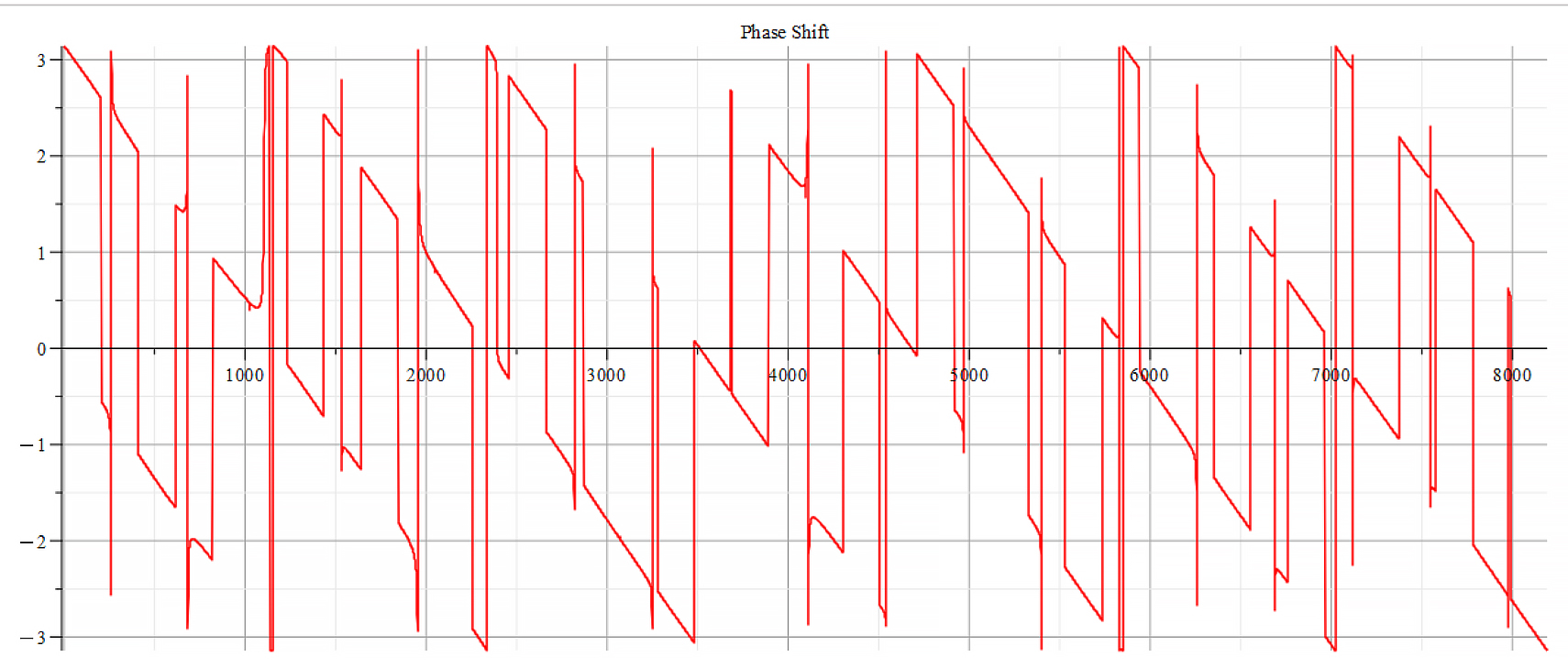
Phase shift for the following parameters:
![Rendered by QuickLaTeX.com \omega={10}^{15}\ [\frac{1}{s}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-40e9be72c982500305e076b28d6e9710_l3.png) ;
; ![Rendered by QuickLaTeX.com E_s={10}^{18}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-c9758917948eb87857658b1f0ac3c81c_l3.png) ;
; ![Rendered by QuickLaTeX.com E_f={5\ 10}^{21}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-26b9acb5d123063310834690dff0970a_l3.png)
For -Ef
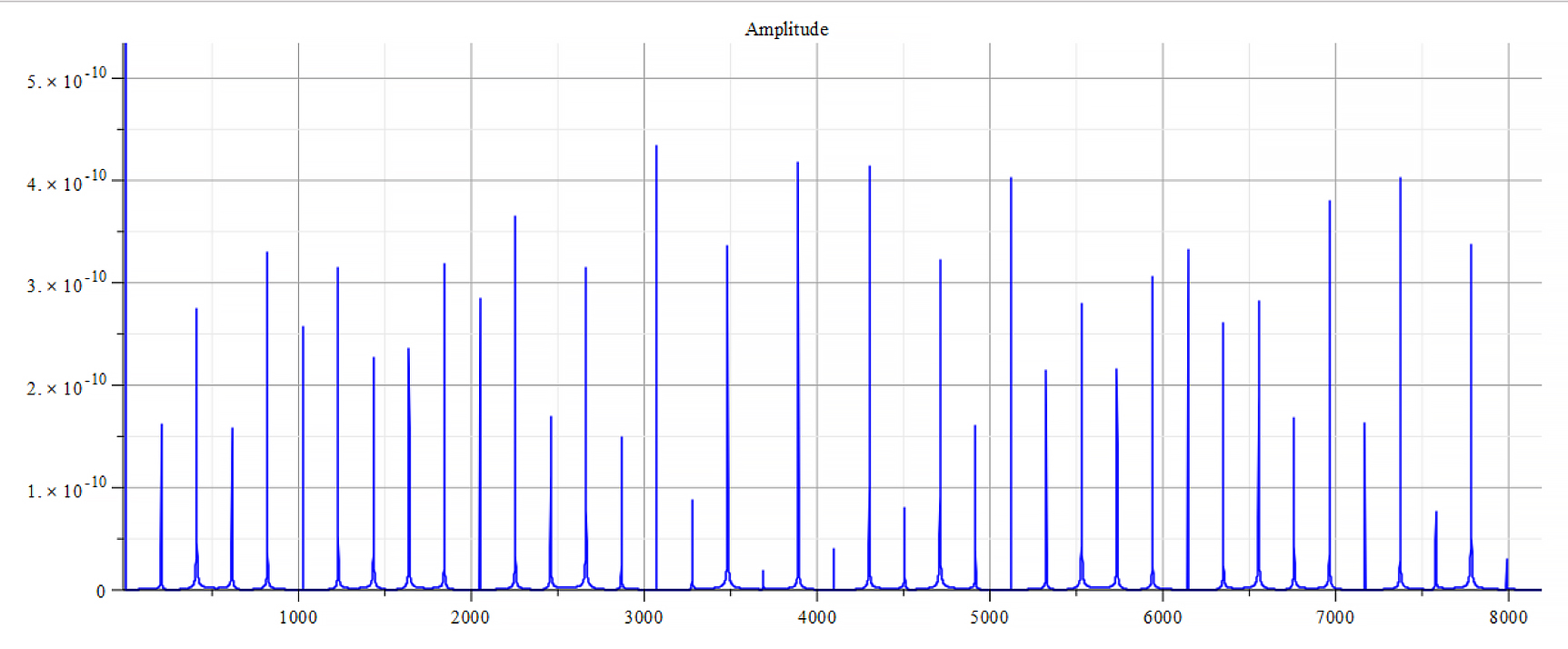
Frequency spectrum for the following parameters:
![Rendered by QuickLaTeX.com \omega={10}^{15}\ [\frac{1}{s}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-40e9be72c982500305e076b28d6e9710_l3.png) ;
; ![Rendered by QuickLaTeX.com E_s={10}^{18}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-c9758917948eb87857658b1f0ac3c81c_l3.png) ;
; ![Rendered by QuickLaTeX.com E_f={-5\ 10}^{21}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-84f86b3237775602aca06abcfa4a80d4_l3.png)
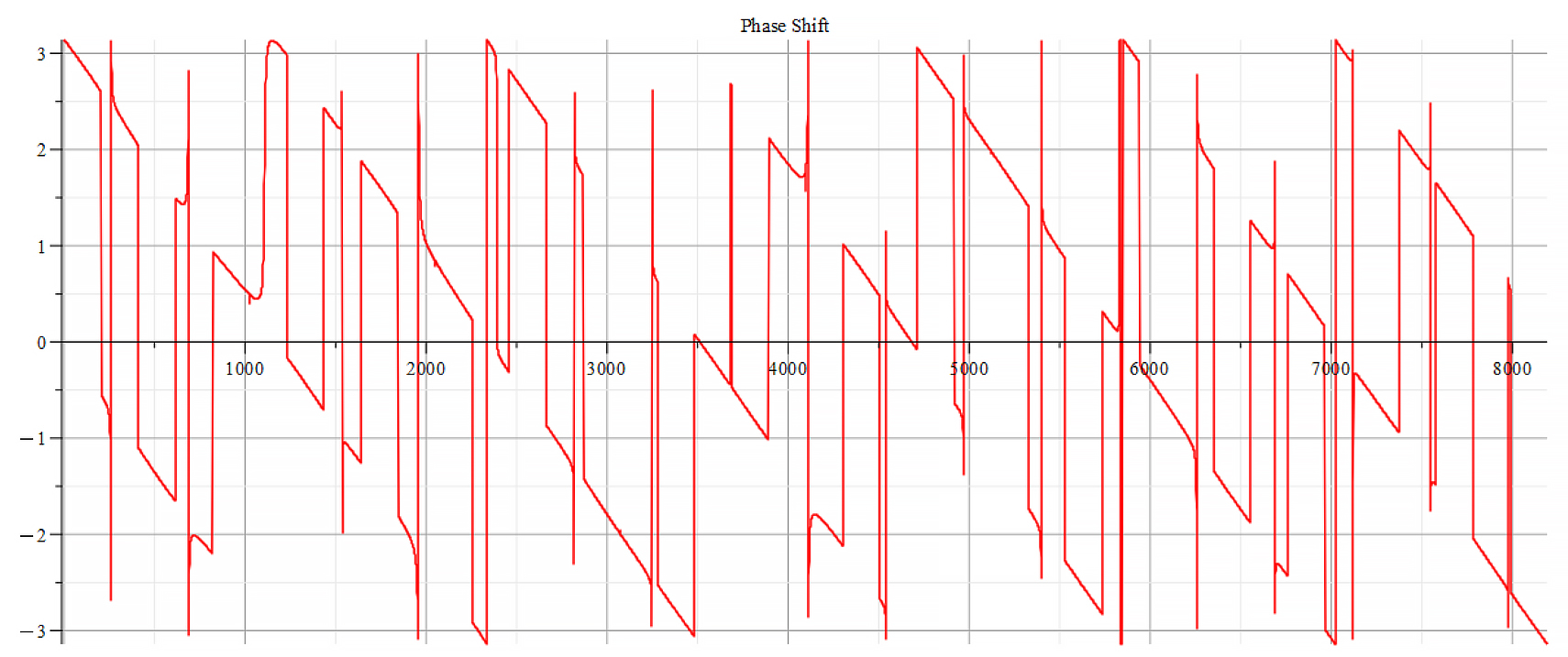
Phase shift for the following parameters:
![Rendered by QuickLaTeX.com \omega={10}^{15}\ [\frac{1}{s}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-40e9be72c982500305e076b28d6e9710_l3.png) ;
; ![Rendered by QuickLaTeX.com E_s={10}^{18}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-c9758917948eb87857658b1f0ac3c81c_l3.png) ;
; ![Rendered by QuickLaTeX.com E_f={-5\ 10}^{21}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-84f86b3237775602aca06abcfa4a80d4_l3.png)
For +Ef
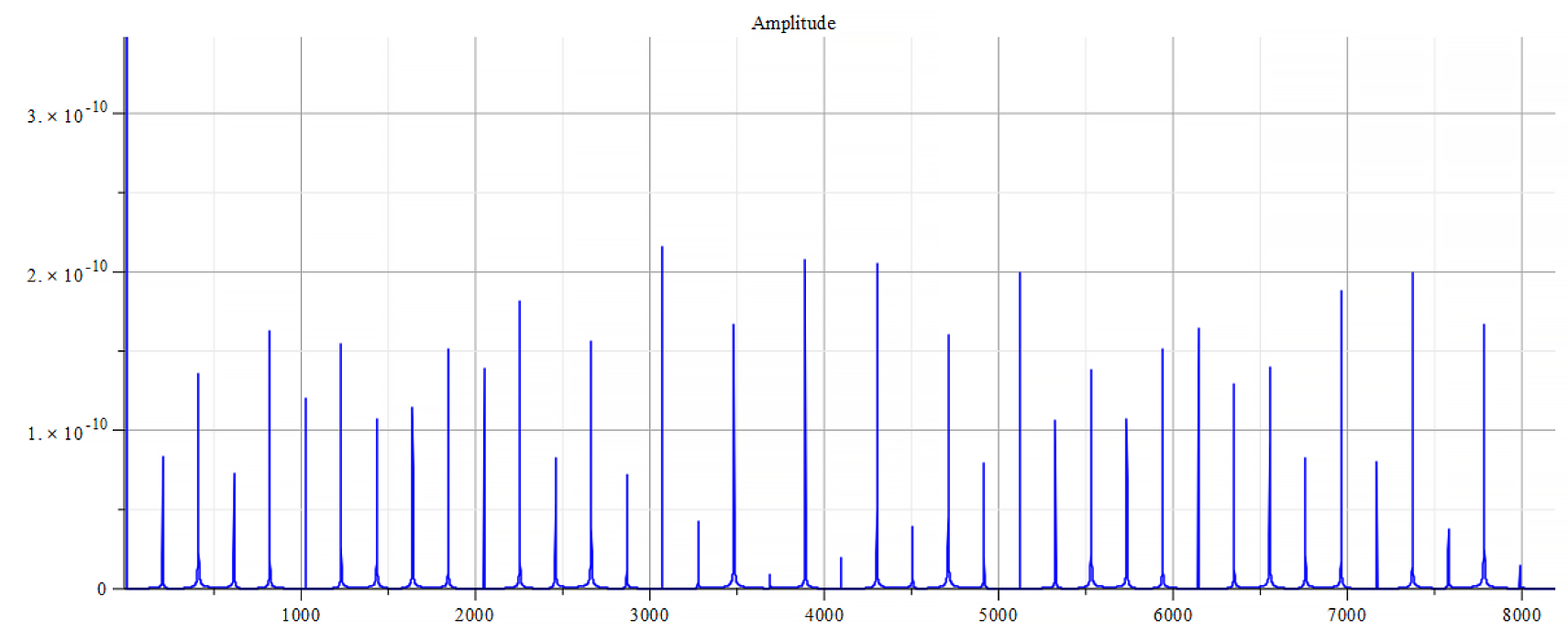
Frequency spectrum for the following parameters:
![Rendered by QuickLaTeX.com \omega={10}^{10}\ [\frac{1}{s}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-3ae6529c3cca5434f07a3e0faceebbb0_l3.png) ;
; ![Rendered by QuickLaTeX.com E_s={10}^{18}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-c9758917948eb87857658b1f0ac3c81c_l3.png) ;
; ![Rendered by QuickLaTeX.com E_f={5\ 10}^{21}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-26b9acb5d123063310834690dff0970a_l3.png)
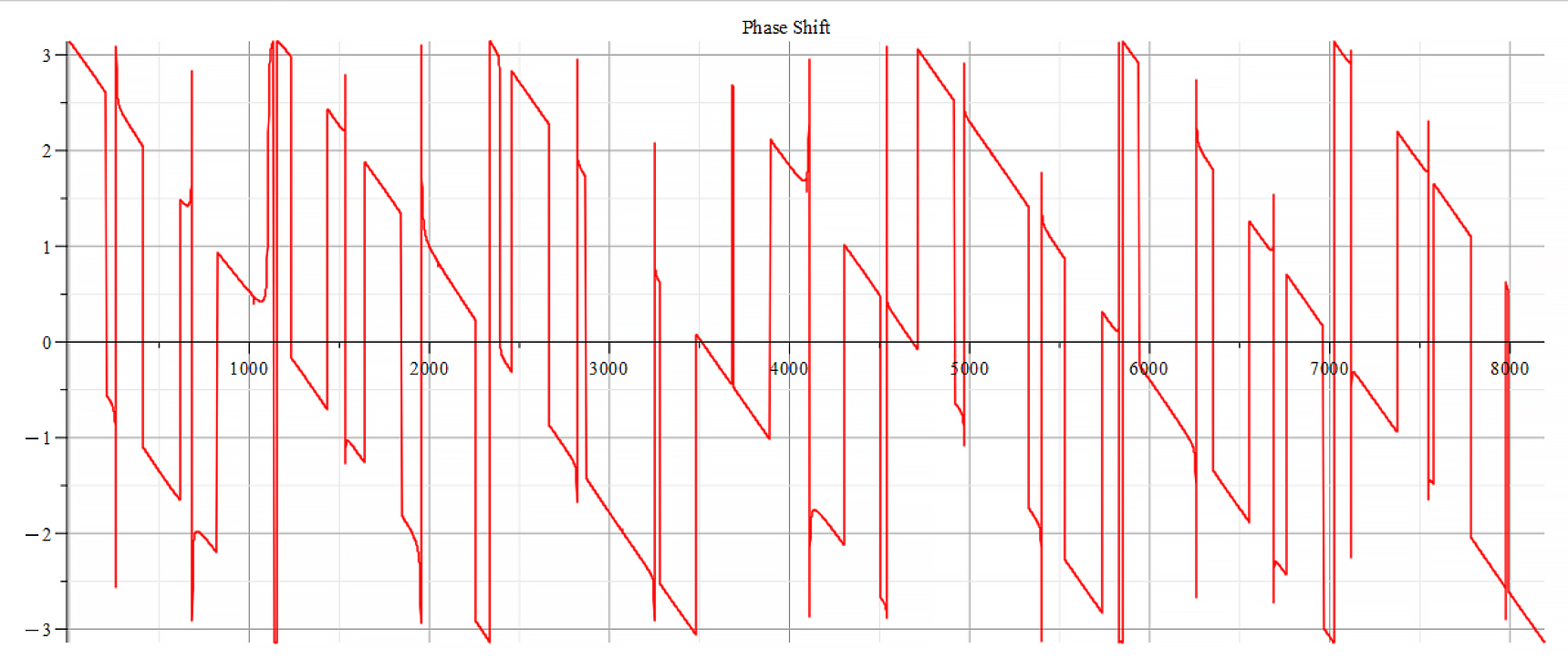
Phase shift for the following parameters:
![Rendered by QuickLaTeX.com \omega={10}^{10}\ [\frac{1}{s}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-3ae6529c3cca5434f07a3e0faceebbb0_l3.png) ;
; ![Rendered by QuickLaTeX.com E_s={10}^{18}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-c9758917948eb87857658b1f0ac3c81c_l3.png) ;
; ![Rendered by QuickLaTeX.com E_f={5\ 10}^{21}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-26b9acb5d123063310834690dff0970a_l3.png)
For -Ef
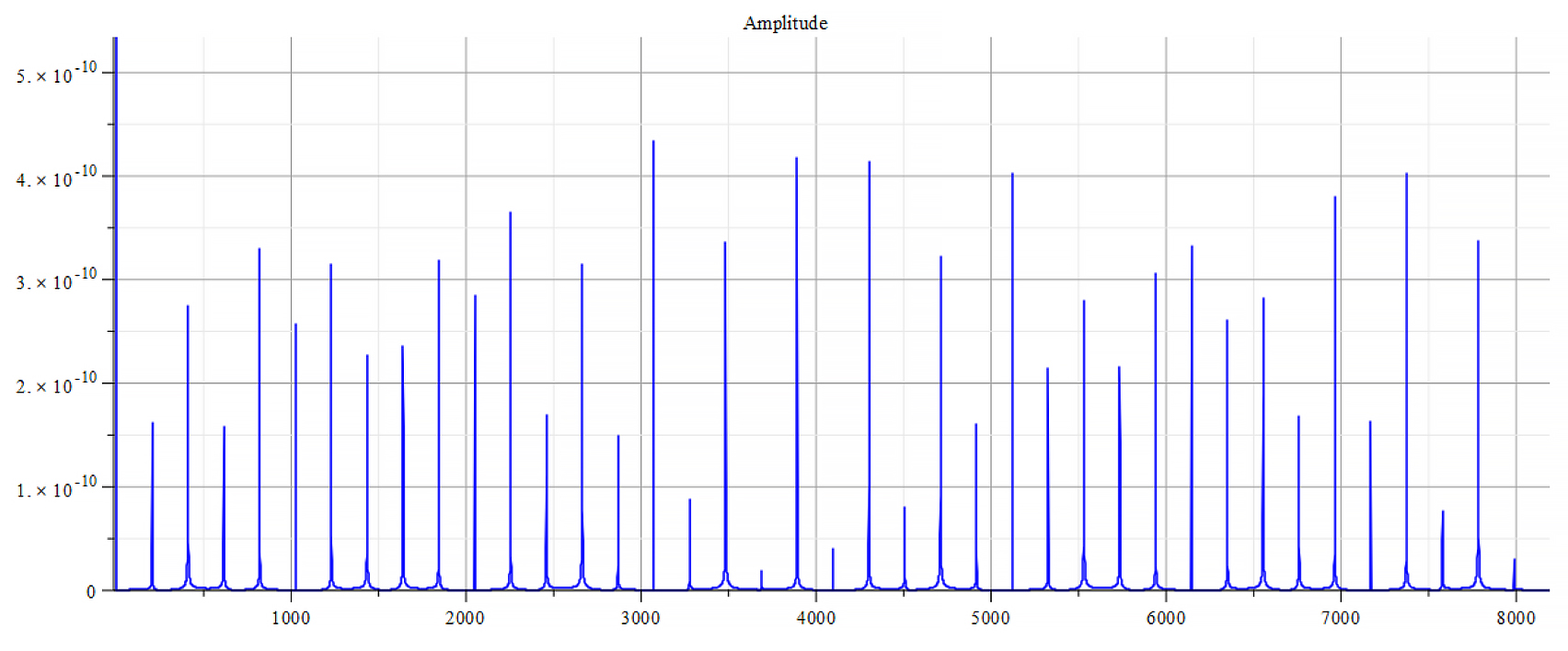
Frequency spectrum for the following parameters:
![Rendered by QuickLaTeX.com \omega={10}^{10}\ [\frac{1}{s}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-3ae6529c3cca5434f07a3e0faceebbb0_l3.png) ;
; ![Rendered by QuickLaTeX.com E_s={10}^{18}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-c9758917948eb87857658b1f0ac3c81c_l3.png) ;
; ![Rendered by QuickLaTeX.com E_f={-5\ 10}^{21}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-84f86b3237775602aca06abcfa4a80d4_l3.png)
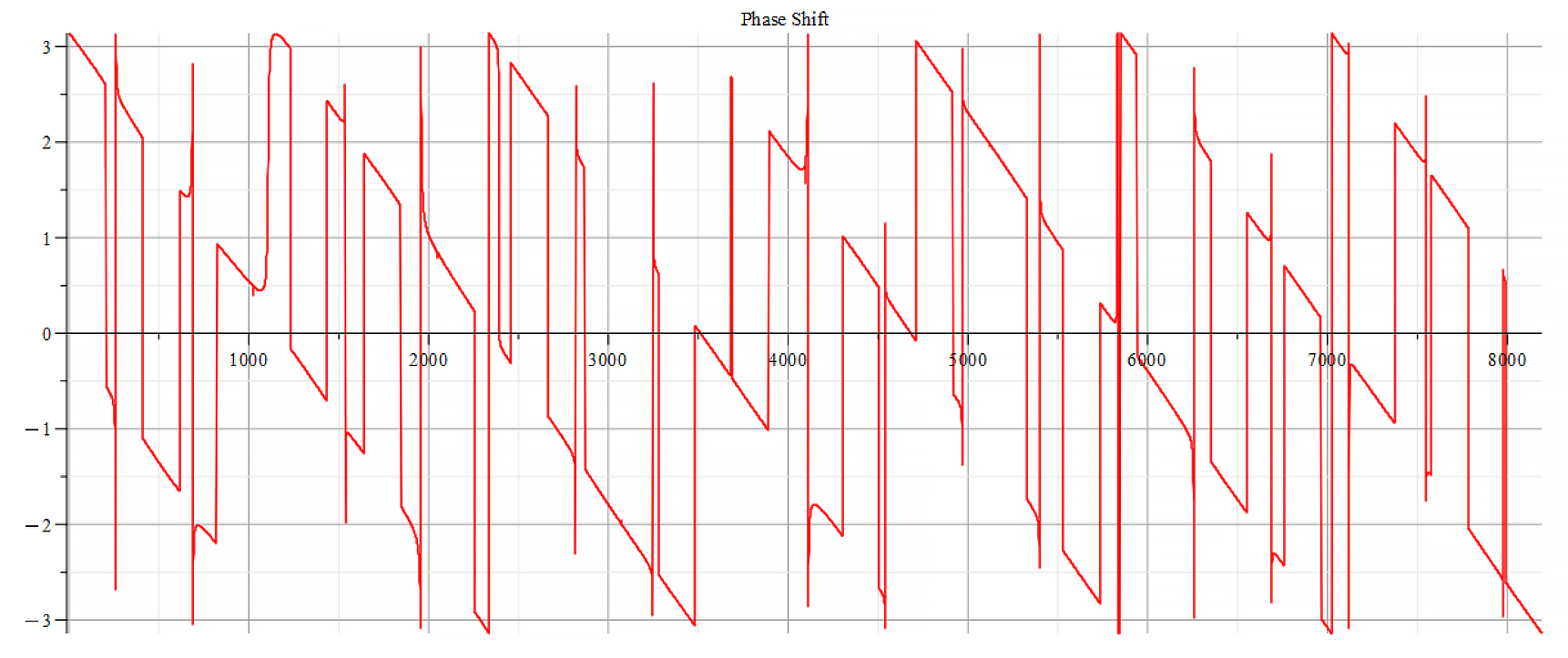
Phase shift for the following parameters:
![Rendered by QuickLaTeX.com \omega={10}^{10}\ [\frac{1}{s}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-3ae6529c3cca5434f07a3e0faceebbb0_l3.png) ;
;![Rendered by QuickLaTeX.com E_s={10}^{18}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-c9758917948eb87857658b1f0ac3c81c_l3.png) ;
; ![Rendered by QuickLaTeX.com E_f={-5\ 10}^{21}\ [\frac{V}{m}]](https://physics-answers.com/wp-content/ql-cache/quicklatex.com-84f86b3237775602aca06abcfa4a80d4_l3.png)
From the Fourier frequency analysis, we see that the main frequency is: ![]() .
.
In general, the main frequency and harmonics are given by the following formula:
![]() ,
, ![]()
III.b Refractive Index Analysis due to a Force caused by a Static Electric Field plus an Electric Signal – Partial or Total Energy Absorption
When the nucleus is under the action of external forces, and if it doesn’t break apart, then we can assume that a dynamic equilibrium state must exist. Under such circumstances, Newton’s second law requires that the sum of forces be equal to zero, ![]() , that is,
, that is,
![]() (9)
(9)
Recall that the net nuclear force has already been written in terms of the index of refraction in Part-1, Eq. (23a):
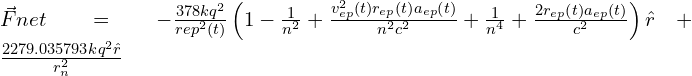
Now we can equate the forces according to Eq. (9), then solve for “n”,
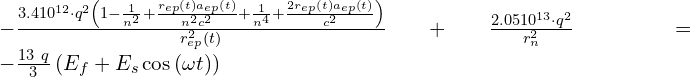 (10)
(10)
The refractive index “n” is a somewhat long-expression which is nonsense to copy here. Some plots as examples are shown below, where the main used parameters are:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]()
 | No graph was obtained due to complex number result |
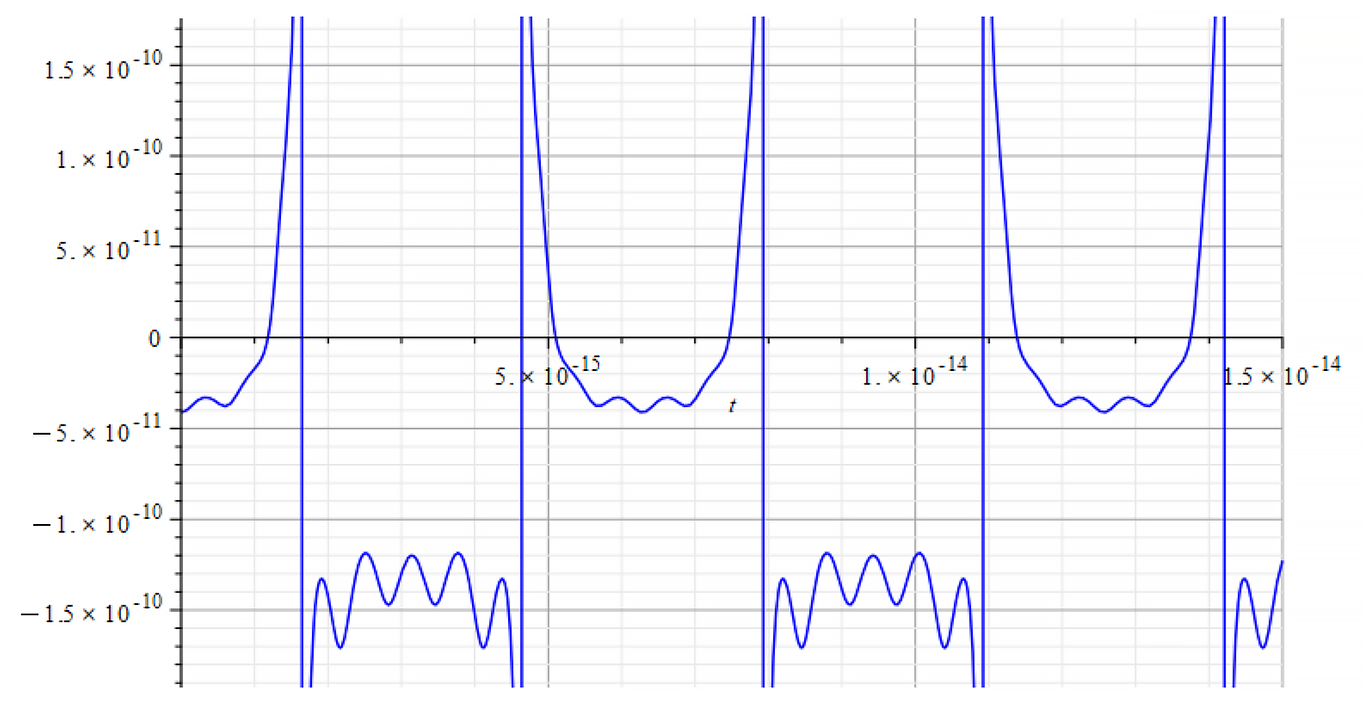
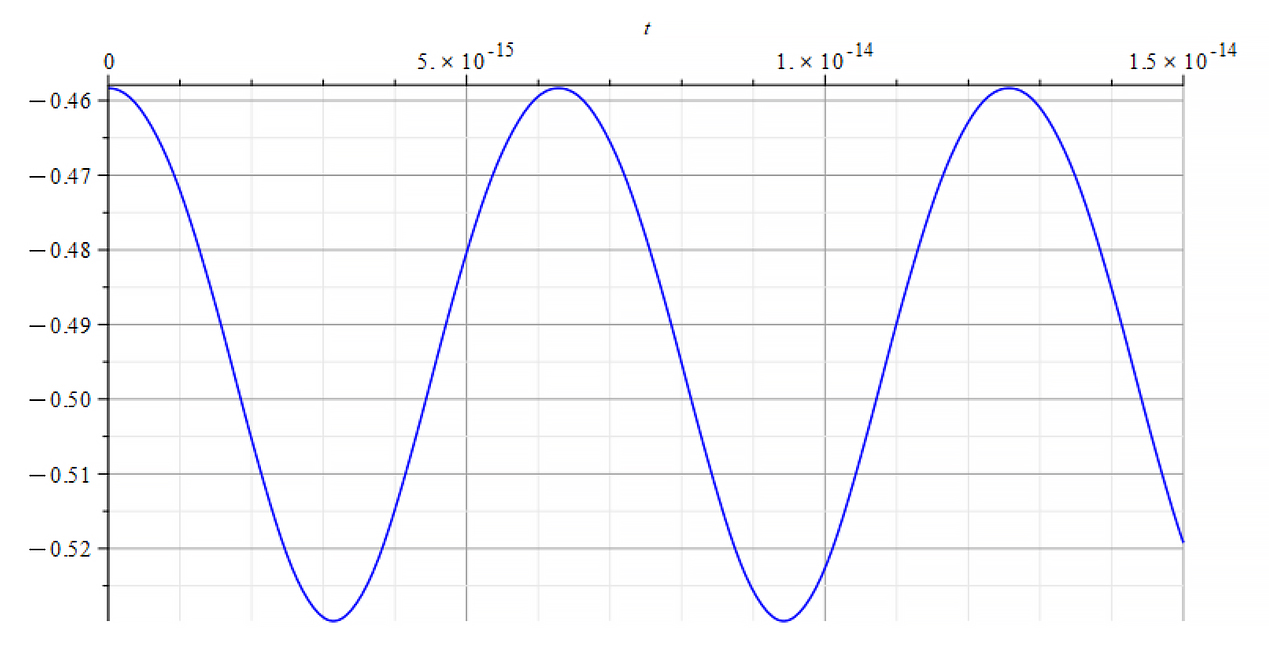
Refractive Index vs. time for the following parameters: | Refractive Index vs. time for the following parameters: |
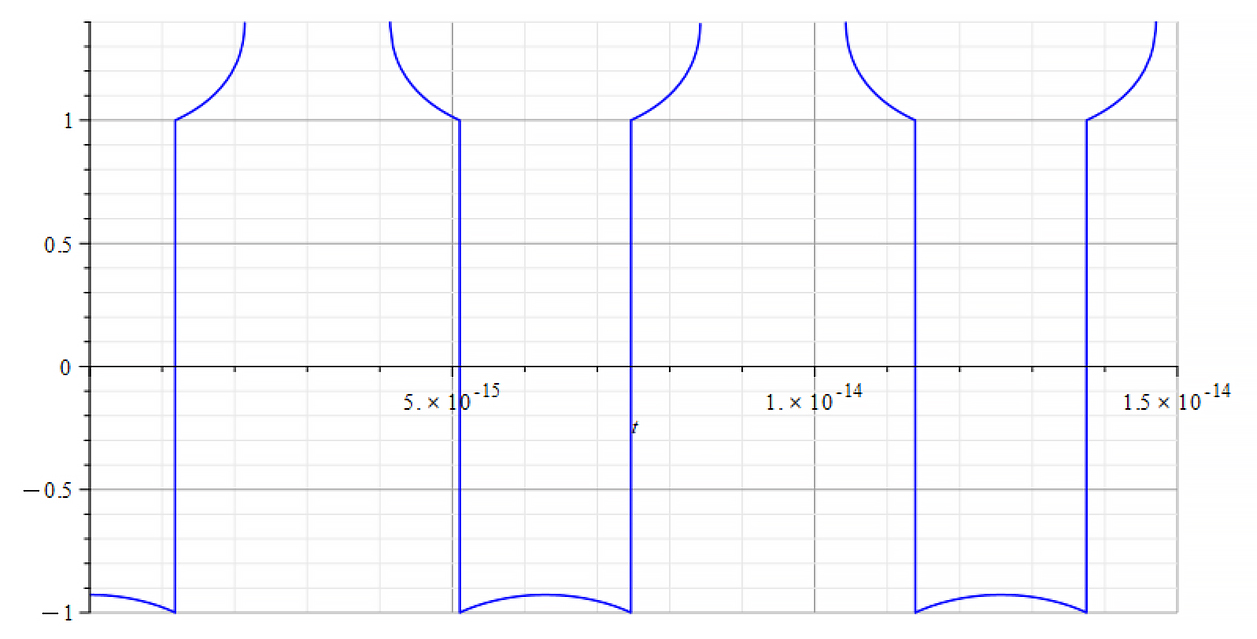 | 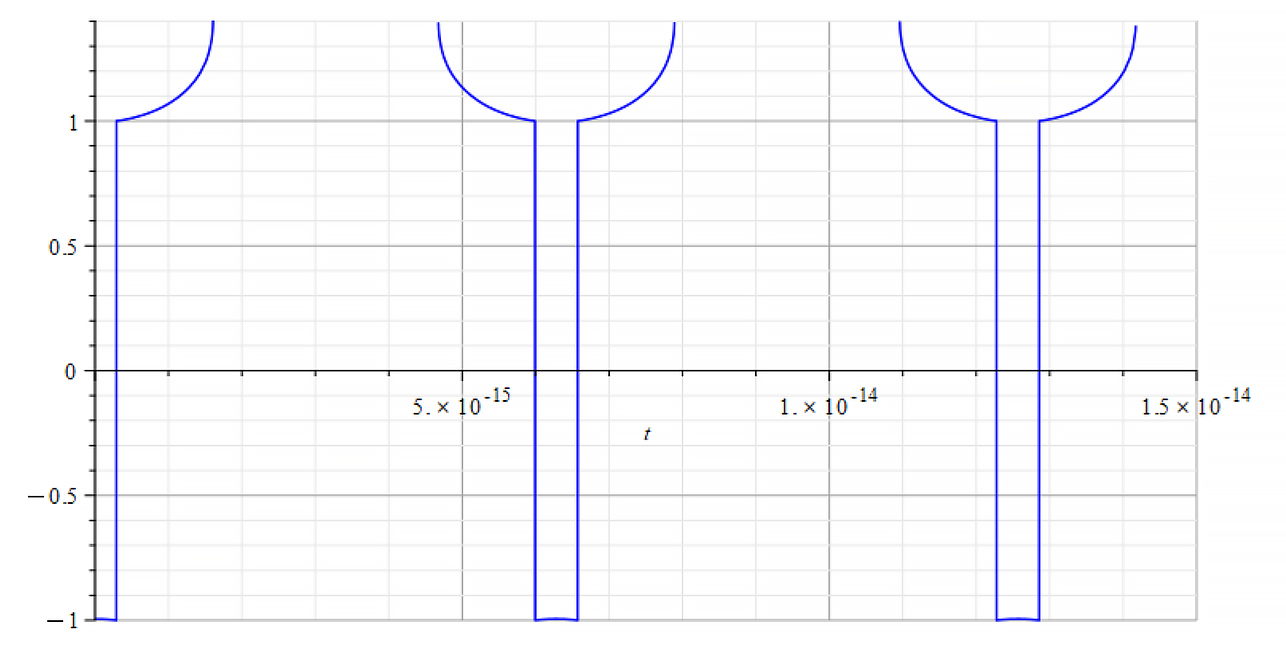 |
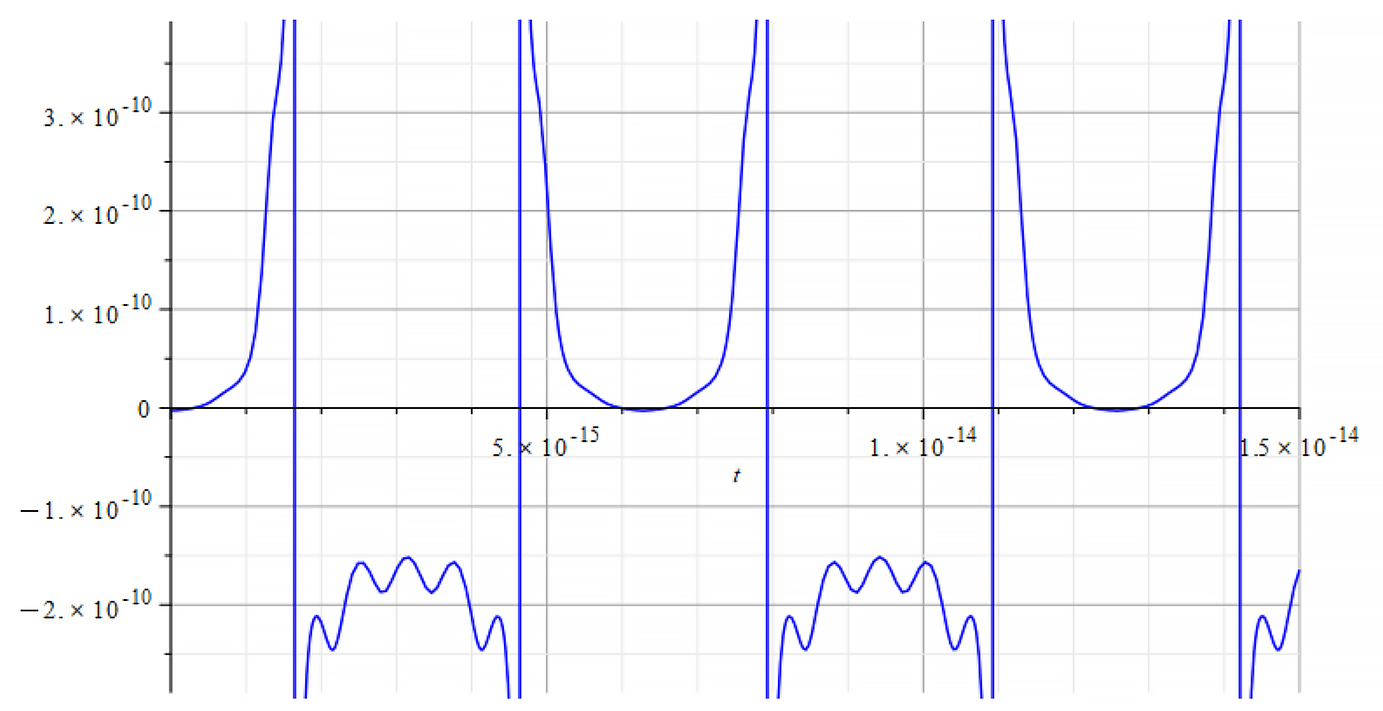
Refractive Index vs. time for the following parameters: | Refractive Index vs. time for the following parameters: |
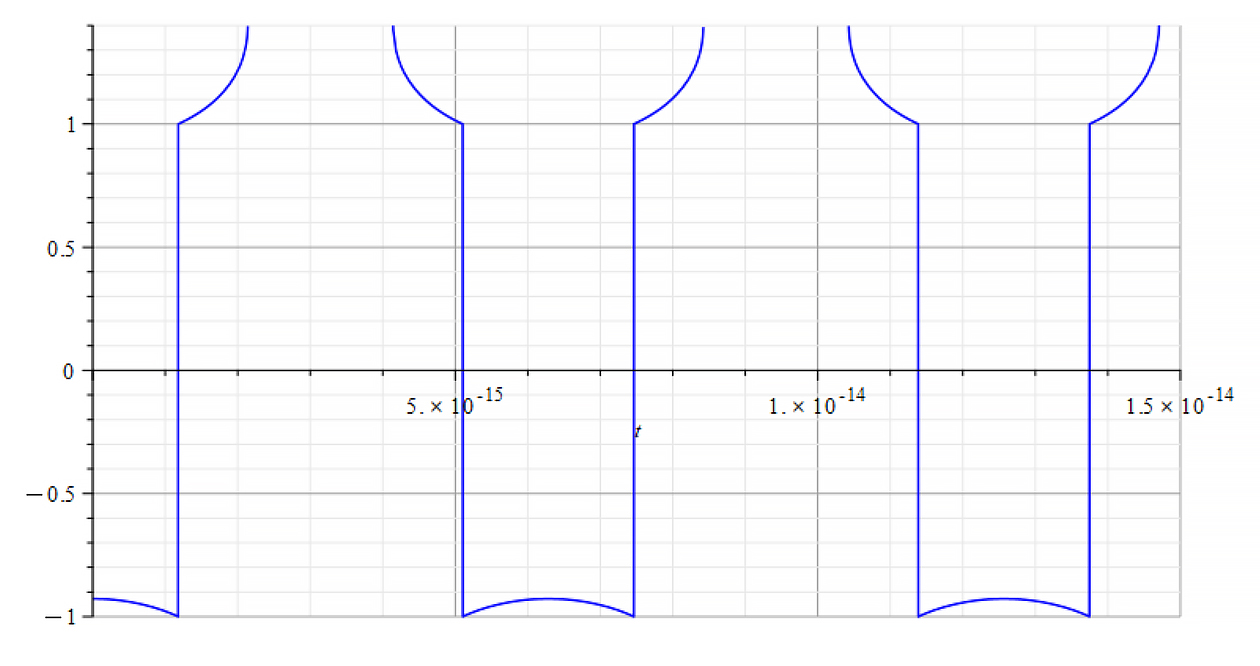 | 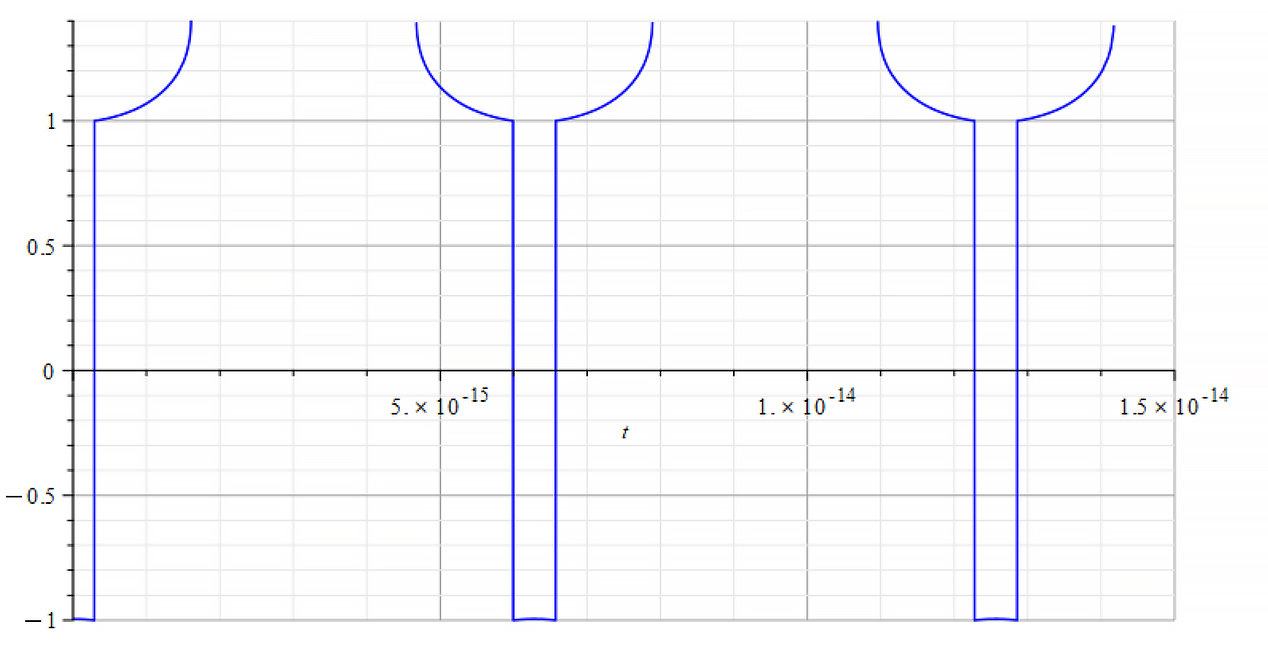 |
Refractive Index vs. time for the following parameters: | Refractive Index vs. time for the following parameters: |
III.c Comparison of Mass with Refractive Index Behavior due to a Force caused by a Static Electric Field plus an Electric Signal – Partial or Total Energy Absorption
To analyze the changes in the refractive index “n” with respect to changes in nuclear mass, overlaid graphs of both quantities are shown below, which uncover interesting results.
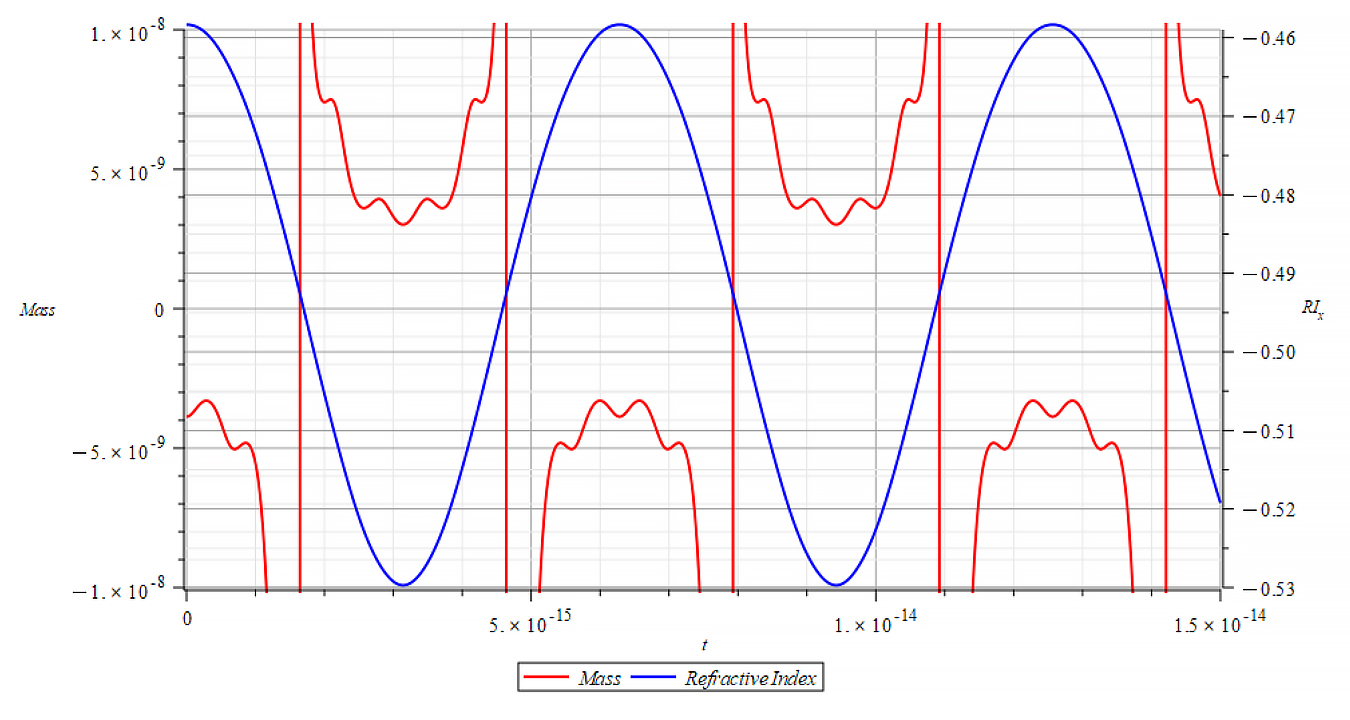 | No graph was obtained due to complex number result in refractive index |
Mass & Refractive Index vs. time for the following parameters: | Mass & Refractive Index vs. time for the following parameters: |
The Refractive Index here is always negative, independent of the mass sign, and oscillates by following the rate of change of the mass. It seems that the refractive index depends on the derivative of the mass, that is
![]()
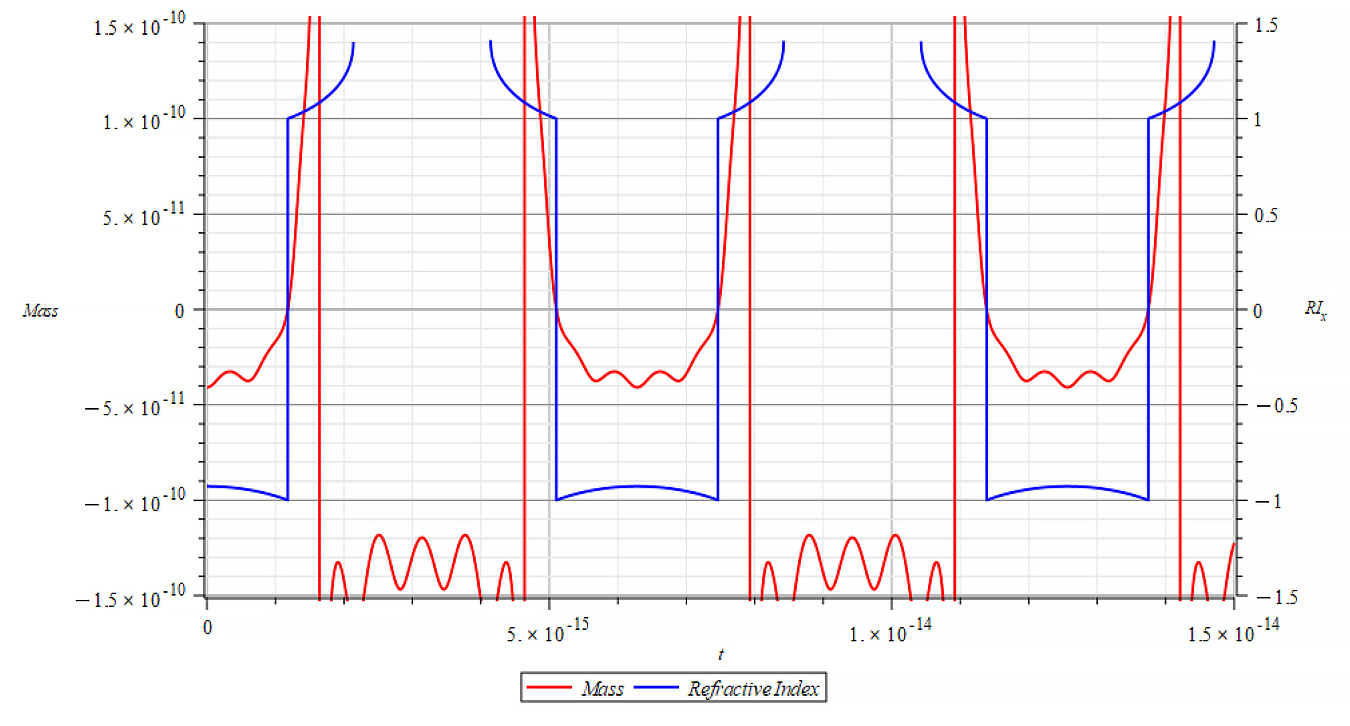 | 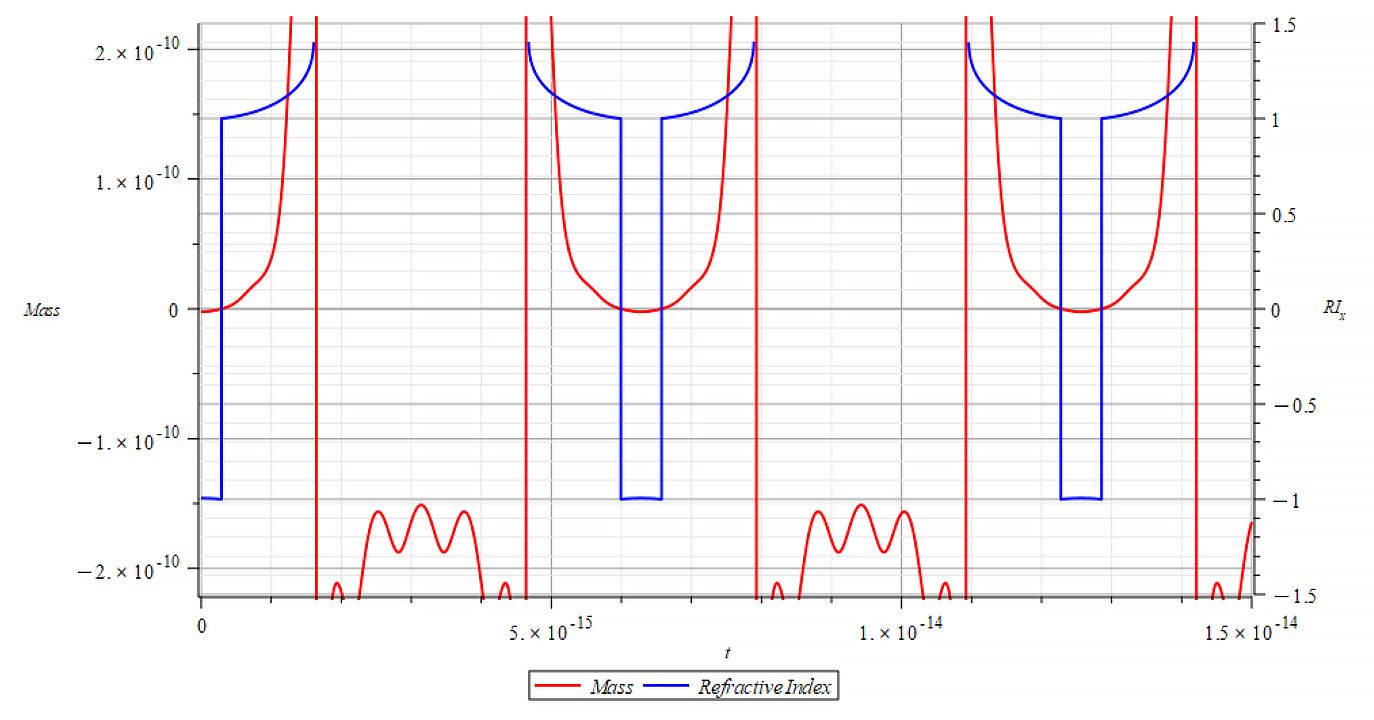 |
Mass & Refractive Index vs. time for the following parameters: | Mass & Refractive Index vs. time for the following parameters: |
Here, the Refractive Index again depends on the slope of the mass plot. It decreases with negative mass slope, and vice versa, until reaching the m=0 point, where abruptly switches between n=±1. It seems that the refractive index depends on the derivative of the mass, that is
![]()
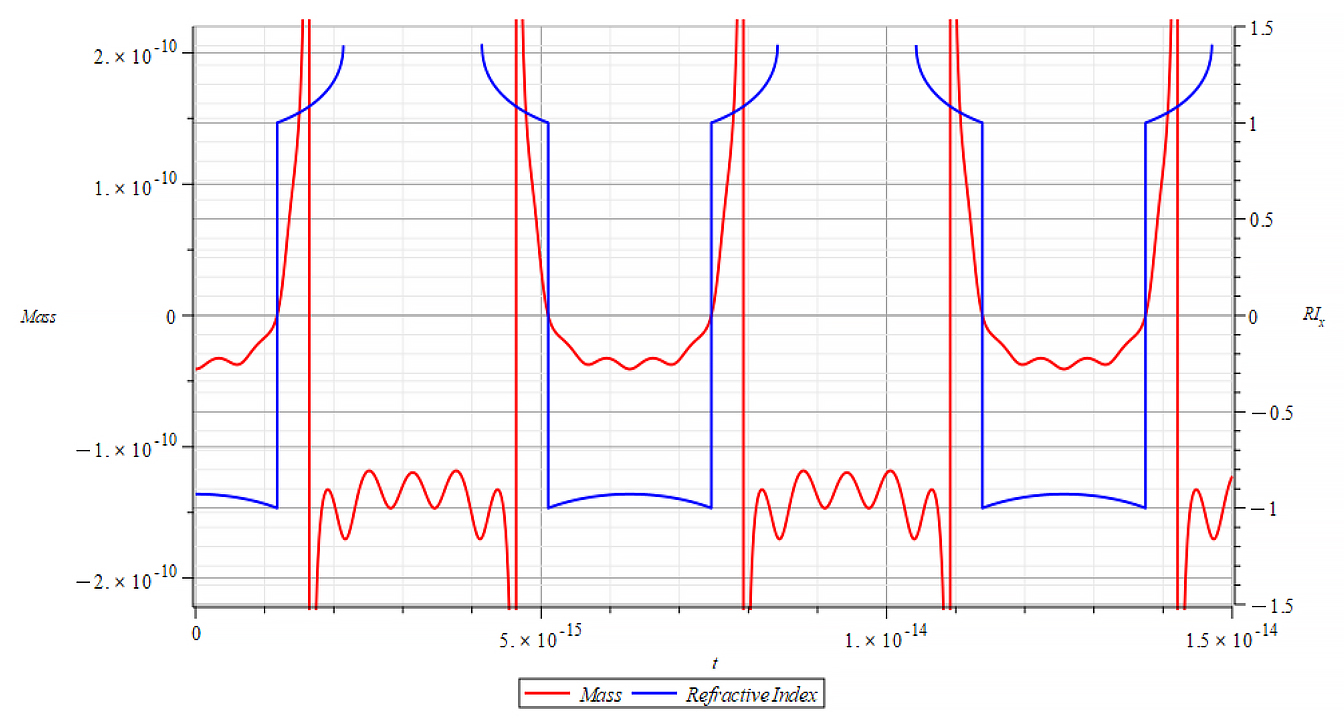 | 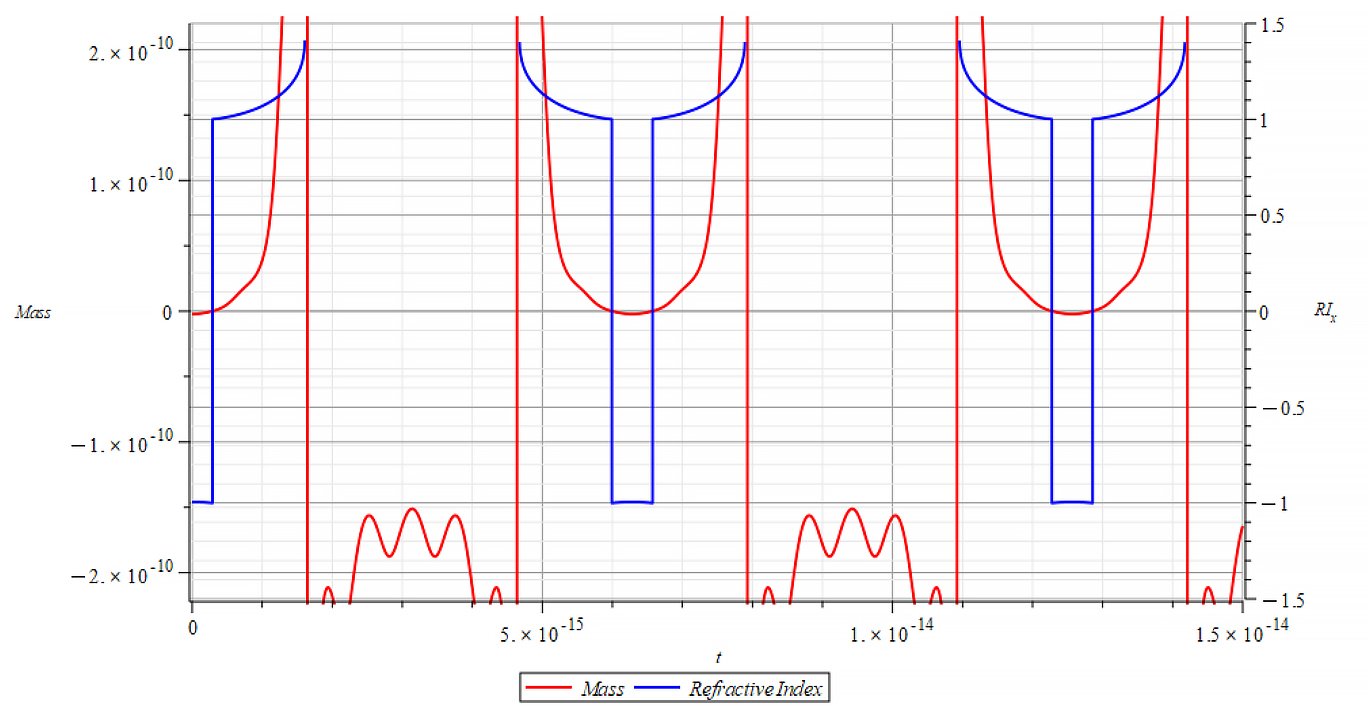 |
Mass & Refractive Index vs. time for the following parameters: | Mass & Refractive Index vs. time for the following parameters: |
Here, the Refractive Index again depends on the slope of the mass plot. It decreases with negative mass slope, and vice versa, until reaching the m=0 point, where abruptly switches between n=±1. It seems that the refractive index depends on the derivative of the mass, that is
![]()
This is an important result that tells us that the refractive index behavior is like a “beacon”, signaling the zones of the negative mass regime, as well as the points of mass changes.
Conclusions
It has been demonstrated that the application of the Universal Electrodynamic Force to the new Atomic Model predicts important changes in nuclear mass when an external force caused by an Electric Signal with an added Static Electric Field is acting on the atomic nucleus.
As we have demonstrated in previous papers, mass is an electrodynamic quantity and as such, it can be manipulated at will. It was demonstrated in this paper that besides the previously analyzed external agents, one more mean can be used to achieve mass changes.
It has been demonstrated that the magnitude and the sign of the mass can be modified by changing the amplitude and/or frequency of the external signal, within a certain range, and by modifying the magnitude and sign of the static electric field.
The change of the refractive index values during mass change was also clearly demonstrated. There is clear evidence that the refractive index is proportional to the rate of change of the mass, i.e., to the derivative of mass with respect to time.
The refractive index can be used as an aid to search for the negative mass region of the nucleus, as well as in any piece of “macro” material. The refractive index is a “beacon” that signals the exact point of mass sign change and its range, and any mass changes in general.
Fourier’s analysis shows in the phase shift graphs many swings of phase between ±π, which clearly indicate resonance states in the nucleus at those frequencies, as well interferences with the external agent.
In previous papers, we described that the main force that keeps the nuclear shell in a very tight packing structure in such a tiny space is the electrostatic force. This is really an enormous force. It means that we also need huge external electromagnetic fields to achieve some nuclear interaction, and this may represent a technical limitation in the present time.
Bibliography
[1]. Shanshan Yao, Xiaoming Zhou and Gengkai Hu, “Experimental study on negative effective mass in a 1D mass–spring system” (2008), New Journal of Physics (2008). https://iopscience.iop.org/article/10.1088/1367-2630/10/4/043020/pdf
[2]. J. P. Wesley, “Inertial Mass of a Charge in a Uniform Electrostatic Potential Field” (2001), Annales Foundation Louis de Broglie, Volume 26, nr. 4 (2001).
[3]. V. F. Mikhailov, “Influence of an electrostatic potential on the inertial electron mass” (2001), Annales Foundation Louis de Broglie, Volume 26, nr. 4 (2001).
[4]. M. Weikert and M. Tajmar, “Investigation of the Influence of a field-free electrostatic Potential on the Electron Mass with Barkhausen-Kurz Oscillation” (2019), ), Annales Foundation Louis de Broglie, Volume 44, (2019).
[5]. Timothy H. Boyer, “Electrostatic potential energy leading to a gravitational mass change for a system of two point charges” (1979), American Journal of Physics 47, 129 (1979), https://aapt.scitation.org/doi/10.1119/1.11881
[6]. A. K. T. Assis, “Changing the Inertial Mass of a Charged Particle” (1992), Journal of the Physical Society of Japan Vol. 62, No. 5, May, 1993, pp. 1418-142, https://journals.jps.jp/doi/abs/10.1143/JPSJ.62.1418?journalCode=jpsj
[7]. M. Tajmar, “Propellantless propulsion with negative matter generated by electric charges” (2013), Technische Universität Dresden (2013), https://tu-dresden.de/ing/maschinenwesen/ilr/rfs/ressourcen/dateien/forschung/folder-2007-08-21-5231434330/ag_raumfahrtantriebe/JPC—Propellantless-Propulsion-with-Negative-Matter-Generated-by-Electric-Charges.pdf?lang=en
[8]. M. Tajmar and A. K. T. Assis, “Particles with Negative Mass: Production, Properties and Applications for Nuclear Fusion and Self-Acceleration” (2015), https://www.ifi.unicamp.br/~assis/J-Advanced-Phys-V4-p77-82(2015).pdf
[9]. M. A. Khamehchi, Khalid Hossain, M. E. Mossman, Yongping Zhang, Th. Busch, Michael McNeil Forbes, and P. Engels, “Negative-Mass Hydrodynamics in a Spin-Orbit–Coupled Bose-Einstein Condensate” (2017), Phys. Rev. Lett. 118, 155301 (2017), https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.118.155301
[10]. David L. Bergman, J. Paul Wesley, “Spinning Charged Ring Model of Electron Yielding Anomalous Magnetic Moment” (1990).
[11]. Joseph Lucas and Charles W. Lucas, Jr., “A Physical Model for Atoms and Nuclei”, Galilean Electrodynamics, Volume 7, Number 1 (1996), Foundations of Science (2002-2003), Part 1, Part 2, Part 3, Part 4.
[12]. Charles W. Lucas, Jr., “Derivation of the Universal Force Law”, Foundations of Science (2006-2007), Part 1, Part 2, Part 3, Part 4.
[13]. Arthur H. Compton, “The size and shape of the electron” (1918), Journal of the Washington Academy of Sciences, Vol. 8, No. 1, https://www.jstor.org/stable/24521544
[14]. David L. Bergman, “Modeling the Real Structure of an Electron” (2010), Foundations of Science.
[15]. David L. Bergman, “Shape & Size of Electron, Proton & Neutron” (2004), Foundations of Science.
[16]. Zoran Jaksic, N. Dalarsson, Milan Maksimovic, “Negative Refractive Index Metamaterials: Principles and Applications” (2006), https://www.researchgate.net/publication/200162674_Negative_Refractive_Index_Metamaterials_Principles_and_Applications
Related articles:
Negative Mass and Negative Refractive Index in Atom Nuclei – Nuclear Wave Equation – Gravitational and Inertial Control <Part-3>
Negative Mass and Negative Refractive Index in Atom Nuclei – Nuclear Wave Equation – Gravitational and Inertial Control <Part-6>
What is Charge? – The Redefinition of Atom – Energy to Matter Conversion
