Raul Fattore
May 27, 2024
This study is divided into four parts
Table of Contents
Summary of Part 4
The study reveals the attraction force between charges of equal sign in a negative mass regime, offering advantages over current nuclear fusion projects. It analyzes the mass behavior of reactants and shows the negative mass operating region. New reactions are calculated under this regime, potentially increasing the standard released energy. A proposed “negative mass nuclear fusion cell” is suggested as a simple and affordable alternative for electricity generation.
Abstract
The increasing need for energy by mankind over time has led to climate change problems and, most importantly, human health issues due to the storage of radioactive waste that lasts a very long time, thus affecting future generations.
Advances in atomic and nuclear physics several years ago promised a revolution in energy production, offering a significant advantage over burning coal, gas, or oil. Unfortunately, scientists at that time did not make use of their brains appropriately. They simply misused and wasted all the advanced knowledge acquired in atomic and nuclear physics to just boil water!
Nuclear fusion was “reborn” as an alternative to generate energy that might be “clean” for the environment, with “minimum” radiation risks for mankind and no radioactive waste. Clean energy generation and radiation-free risks can only be guaranteed by using certain technology for nuclear fusion.
Making a fusion reaction happen is not complicated (like 14-year-old Taylor Wilson did in his home in 2008). However, there are two main problems with nuclear fusion that have prevented it from being commercially viable until now:
- Efficiency
- Safety
Currently, most scientists experimenting with nuclear fusion are making serious mistakes. They are using costly devices and wasting vast amounts of energy in an attempt to replicate conditions found in stars on Earth, with no encouraging outcomes to date. Why? Fusions in stars are processes that are fully determined by probability, so you cannot build a project just on them. Probability is not the same as certainty, even when it represents the likelihood that an event will occur.
Negative mass calculations can provide certainty regarding an effective head-on collision of charges, but scattering cross-section calculations cannot.
Nuclear fusion can be greatly eased by negative mass. I refer the reader to the series of articles about Negative Mass in Atom Nuclei [1] to understand how we can have negative mass behavior in nuclei.
- Is nuclear fusion enhanced with negative mass nuclei and particles?
- Can negative mass nuclear fusion be made efficient?
- Can negative mass nuclear fusion offer better safety?
- Does negative mass nuclear fusion rely on statistical processes?
- Does negative mass nuclear fusion offer a simpler and cheaper method to generate energy?
In the development of this study, you’ll find comprehensible answers to the above questions, which are backed by the experimentally proven laws of electrodynamics through the Universal Electrodynamic Force and the New Atomic Model.
Introduction
Nuclear fusion is an extremely fast and violent event that involves the acceleration of charges, whether they are nuclei or single charges. Therefore, scientists should not lose sight of the fact that in any atomic and nuclear interaction, we are dealing with accelerated electric charges.
As such, radiation is always present in any nuclear fusion reaction. No exception.
Due to the huge acceleration of the charges, the spectrum may easily range from X-rays to the most powerful gamma radiation. This radiation can be used in our favor to generate electric energy [9]. However, if this radiation is not properly handled, it will be harmful for human health.
For simplicity, the radiation symbols will be omitted in most of the reaction calculations throughout this study. However, as radiation is always present in any nuclear fusion, from X-ray to gamma, the right way to write a reaction should be to include the radiation symbols as part of the fusion products: A+B\ \rightarrow\ C+D\ +\ \left(X,\ \gamma\right).
Unfortunately, scientists are making deficient calculations of the released energy during nuclear fusion. Why?
Because they use wrong formulas that don’t give the total energy of the system, like the known Einstein’s formula E=\Delta m\ c^2 for mass excess/defect calculations. This formula only gives a result for rest mass energy (potential energy), which should be equivalent to the acquired kinetic energy, but it gives no clues about acceleration. The Einstein energy formula is flawed even in its “relativistic” form since, as in classical mechanics, acceleration is entirely disregarded.
The total energy in a fusion reaction is always higher than the results given by Einstein’s formulas for rest energy and the calculations of kinetic energy from classical mechanics.
Most of the energy values for nuclear fusion given in the scientific literature are deficient because none of them consider radiation energy, which on occasion may be much higher than kinetic energy alone.
Applying Einstein’s formulas and classical mechanics’ kinetic energy calculations to nuclear fusion is extremely risky, since you can never be certain of the amount of radiation generated during a reaction.
The scientific community must be aware when using those formulas because:
• They only give partial energy values.
• They are not compatible with a system of charges.
Those formulas may only be applied to limited, simple mechanical interactions between uncharged bodies.
The derivation of the total energy for a system of charges made in this study will provide scientists with a powerful formula to make real energy calculations in any nuclear fusion reaction and many other applications that involve the interaction of charges.
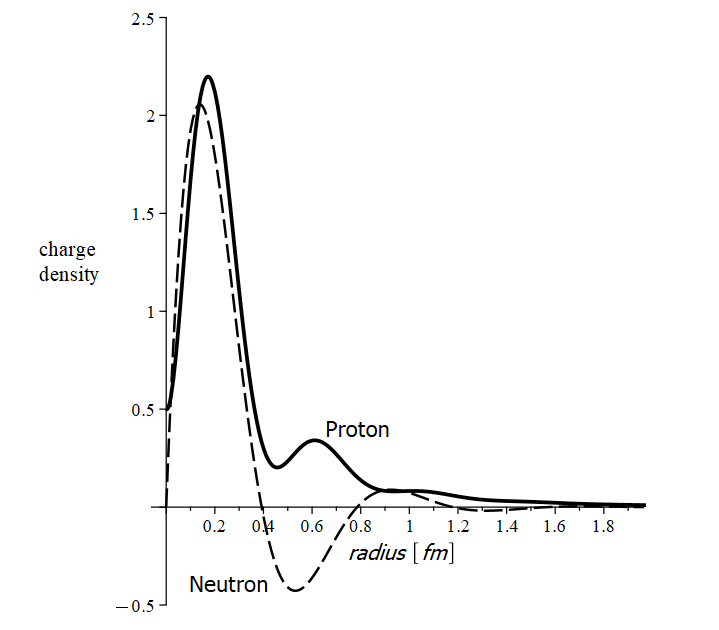
Charge density of the proton and neutron
There are no “neutral particles”. The so-called “neutral particles” are composed of charges that balance the net result [2]. An example of such a particle is the neutron.
Neutrons are stable in the nucleus. However, outside the nucleus, the neutron decays into a proton and an electron with a half-life of fewer than 15 minutes. The mass of the neutron is the sum of the masses of the electron and proton. The neutron has a charge density that varies between positive and negative with respect to its radius (Fig. 1). These facts suggest that the neutron might not be a valid elementary particle but a bound combination of an electron and a proton [3].
Accordingly, the new atomic model precisely describes how electrons and protons are very tightly packed in shells in the nucleus due to the balance of electromagnetic forces.
Based on the energy calculations I made for the Deuterium-Tritium fusion, the binding energy (potential energy) of the electron-proton pair that makes the neutron should be E=-2.127\ MeV when in the nucleus. Outside the nucleus, this energy is given off (radiation, kinetic) during neutron decay time, which unbinds the electron-proton pair.
Because the neutron is always regarded as a “neutral” particle, scientists’ calculations of nuclear reactions and stray reactions may only be partially accurate. The electron and proton may take part in reactions with nuclei or with other electrons and protons when the electron-proton pair that built the neutron unbinds. While some of these reactions will produce energy, others may use some of the system’s energy to generate the fuel for fusion.
As far as I know, these “additional” reactions were never mentioned in any scientific paper. However, some of them could be of such importance that they cannot be ignored and must be considered in calculations, as will be demonstrated in the development of this study.
Since the neutron is one of the fusion products in several reactions and usually carries a high level of kinetic energy and radiation energy, we might be able to use these facts and the internal structure of the neutron in our favor.
The fact that the neutron is a composite of two charges means that we may expect a radiation spectrum from X-rays to gamma rays when the particle is in positive or negative accelerated motion. This is additional energy that we may harvest from the “neutron”, which can be converted into electricity, besides the charges themselves.
Nuclear Fusion With Negative Mass Reactants
In the series of articles on Negative Mass in Atom Nuclei [1], you will find an exhaustive study of the methods that can be used to make the atomic nucleus behave as if its effective mass were negative.
The extremely close packing of protons and electrons in nucleus shells as a result of the balance of electromagnetic forces is described in detail by the new atomic model.
We can safely assume that the distance between shells is tiny due to the extremely tight packing configuration of the particles and that the electrostatic force is the primary force in the nucleus. The equilibrium distance between each shell will be somewhat influenced by the weaker magnetic forces.
The Universal Electrodynamic Force states that mass is a function of the elementary charges as well as the oscillations’ amplitude and frequency, rather than being a constant. Its sign can be changed, its value can be changed at will, it can be made null, and it can be made to take on any magnitude. Consequently, we are no longer able to believe that mass is a fundamental quantity.
When the mass is negative, the direction of the acceleration is opposite that of the force.
Nuclei are composed of charges, and as such, they will always have a predominant charge sign. By making them behave as having negative mass, nuclei with the same polarity will attract each other. The same will happen for single charges.
This opens up new possibilities not only by facilitating nuclear fusion but also by helping new reactions occur that would not otherwise exist.
Forces acting on equal-sign charges with negative mass
The interaction force or relative force between two bodies or charges is defined as negative when the charges or bodies are subject to an attraction condition, while a positive relative force describes the opposite condition, or repulsion.
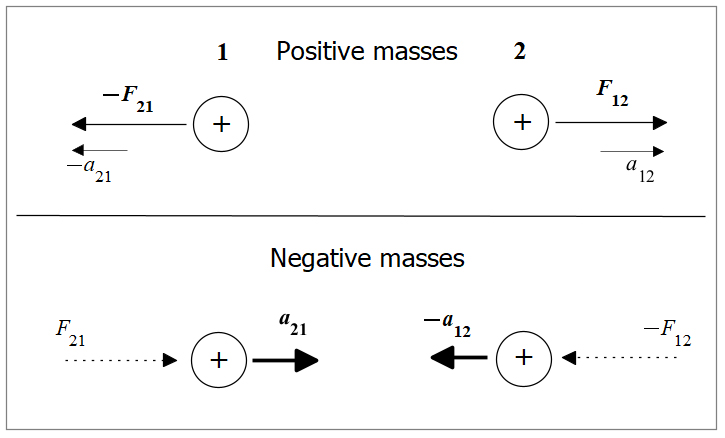
Forces on charges of positive and negative mass
Figure 2 shows two charges of the same sign, with positive masses in the upper part and negative masses in the lower part. The force F_{21} is the force of charge 2 acting on charge 1, while F_{12} is the force of charge 1 acting on charge 2.
The force on one charge is equal to and opposite to the force on the other charge. Both forces constitute an action-reaction pair. Note that the forces pointing left are negative.
Now, let’s write this sign convention for the relative force in terms of the forces that each body or charge causes on the other. In this scenario, the relative force is: F_r=\left(F_{12}-F_{21}\right). The relative force is positive in the repulsion state, and negative in the attraction state.
For two charges of the same sign to attract each other, they must have negative masses. As explained in this article, a particle with negative mass will accelerate in the opposite direction of the acting force. To visualize this behavior, suppose that two charges of the same sign have each an inertial mass m_1 and m_2. The electrostatic force on each charge can then be written as follows: {\vec{F}}_{12}=\frac{Kq_1q_2}{r^2}=m_2\cdot{\vec{a}}_{12}, and -{\vec{F}}_{21}=\frac{Kq_1q_2}{r^2}=m_1\cdot{\vec{a}}_{21}.
The relative force equation clearly shows the repulsion state: F_r=\left(\left(F_{12}\right)-\left(-F_{21}\right)\right)=+\left(F_{12}+F_{21}\right). In this case, the system mass is positive, and the charges are subject to acceleration that points away from each other, by bringing them apart.
Now assume that we can change the mass of each charge from positive to negative. As the electrostatic forces have their origins in the charges, they will remain pointing in the same direction. However, the negative mass will cause the charges to accelerate toward each other in the opposite direction from the acting forces.
Under the negative mass regime, the acceleration on each charge will be {\vec{a}}_{12}=\frac{{\vec{F}}_{12}}{\left(-m_2\right)}, i.e., -{\vec{a}}_{12} and {\vec{a}}_{21}=\frac{-{\vec{F}}_{21}}{\left(-m_1\right)}, i.e., +{\vec{a}}_{21}, as shown in Fig. 2. This change in motion with negative mass happens because the reaction force points in the same direction as the acting force. Mathematically, by matching the signs with the negative mass, we are led to: \left(-{\vec{F}}_{12}\right)=\frac{Kq_1q_2}{r^2}=-m_{sys}\cdot\vec{a}=-\left(-{\vec{F}}_{21}\right), that is -{\vec{F}}_{12}={\vec{F}}_{21}, as shown in Fig. 2, and demonstrated by the relative force between charges: F_r=\left(\left(-F_{12}\right)-\left(F_{21}\right)\right)=-\left(F_{12}+F_{21}\right). This is clearly an attractive force.
As a result, with the negative mass, we have changed a repulsive force into an attractive force between equal sign charges.
How can negative mass help in nuclear fusion?
Usually, a strong electric field suffices to make nuclei and single charges behave as if they have negative mass. The electric field can provide particles with enough acceleration for their head-on collision, which will unavoidably happen.
As charges are attracted by following the motion on the radial line that separates each other, there will be zero probability for a missed collision.
Advantages of negative mass nuclear fusion
Follow below a few advantages that negative mass nuclear fusion may have against current systems.
- Collisions are independent of probability
- No scattering cross section calculations are needed
- New and additional reactions will take place to generate extra energy and even fuel
- There is no need to use expensive equipment
- There is no need for any heat
- There is no need for the supply of extreme amounts of energy
- Cheaper than any current system
Deuterium-Tritium Fusion: Negative Mass by Applying an External Electric Field
The net force for Deuterium-Tritium nuclei during the fusion process was derived in Part 3 and given by Eq. (23):
F_{D-T}=-\frac{5kq^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{5kq^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}After a little algebra, the simplified version of this fusion net force becomes:
F_{D-T}=-\frac{5kq^2}{r^2}+\frac{5kq^2v^2}{r^2c^2}-\frac{10kq^2a}{rc^2} (1)
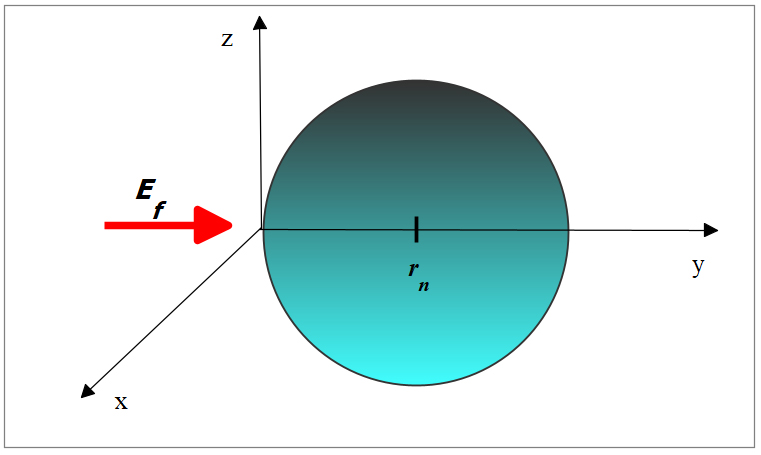
External electric field applied on the nucleus
Assume now that we apply an electric field of magnitude E_f to the “fused” nucleus (Fig. 3), whose net force is given by Eq. (1). The force exerted by this external electric field on the “fused nucleus” is, as usual: F_{ext}=Q\cdot E_f, where “Q” is the net charge of both nuclei.
The net charge for the Deuterium nucleus is 1p, and for the Tritium nucleus 1p. Then, the total net charge is Q\ =2q\ =2\cdot{1.6\ 10}^{-19}C\ =\ {3.2\ 10}^{-19}C.
Applying Newton’s second law to the system created by the two “fusing” nuclei, we have:
\sum F=m_{sys}\cdot a=F_{\mathrm{D}-T}+F_{ext};
m_{sys}=\frac{1}{a}\cdot\left(F_{\mathrm{D}-T}+F_{ext}\right)After replacing the two forces and the net charge “Q” of both nuclei, the mass equation becomes:
m_{sys}=\frac{1}{a}\cdot\left(-\frac{5kq^2}{r^2}+\frac{5kq^2v^2}{r^2c^2}-\frac{10kq^2a}{rc^2}+2q\cdot E_f\right) (2)
Since the electric field is caused by an external electric potential V_f, this potential applied across the “fusing” nuclei is: V_f=E_f\cdot\left(2r_n\right), where 2r_n is the diameter of the fused nucleus. Now we can replace the electric field in Eq. (2), which gives us the final equation of the system mass:
m_{sys}=\frac{1}{a}\cdot\left(-\frac{5kq^2}{r^2}+\frac{5kq^2v^2}{r^2c^2}-\frac{10kq^2a}{rc^2}+2q\cdot\frac{V_f}{2r_n}\right) (3)
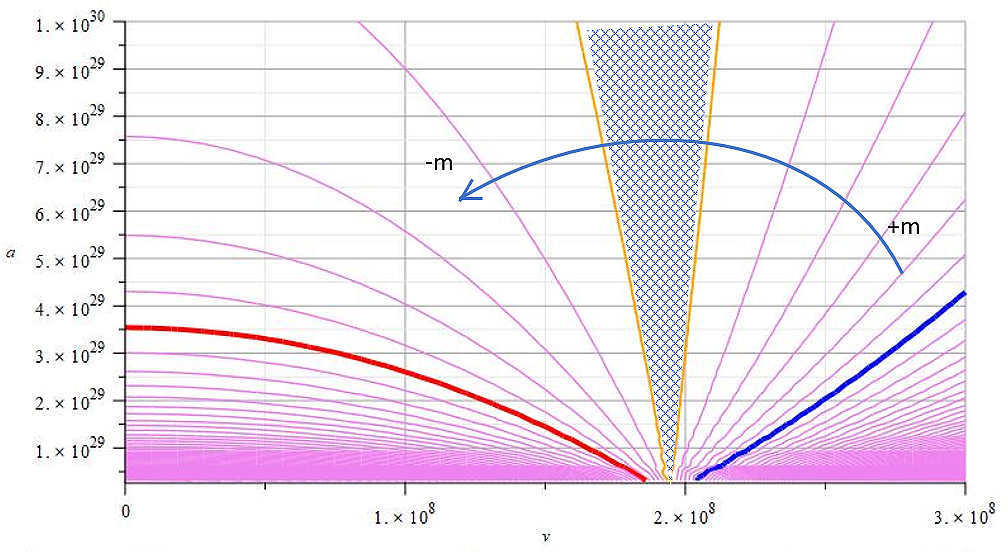
Graph of mass vs. velocity and acceleration showing the regions of negative mass and positive mass and the transition zone for Deuterium-Tritium fusion
The distance between charge centers for the released energy of the fusion was calculated during the analysis of the Deuterium-Tritium fusion made in Part 3, which resulted in r=0.408\ {10}^{-15}m. It seems somewhat logical that we use this value in Eq. (3). The average nucleus radius for Deuterium and Tritium is very similar and is taken as r_n=2\ {10}^{-15}m.
Figure 4 shows a level or contour graph of Eq. (3) for the system mass of the Deuterium and Tritium nuclei with respect to the relative velocity and acceleration, for the following parameters: r=0.408\ {10}^{-15}m, r_n=2\ {10}^{-15}m and V_f=50\ {10}^6V.
As a reference, the masses of the Deuterium and Tritium nuclei, when added, give a total mass of m=8.35\ {10}^{-27}Kg.
The thick blue line corresponds to a mass value m=9.28\ {10}^{-27}Kg, while the mass corresponding to the thick red line is m=-8.3\ {10}^{-27}Kg.
In the blue-shaded area between the two orange lines lies the m=0 vertical line, which gives the transition between positive and negative mass regions. To avoid “lines’ jam” in the plot, only a few level lines are shown. The mass corresponding to the right orange line is m=4.87\ {10}^{-28}Kg, while the mass given by the left orange line is m=-9.78\ {10}^{-28}Kg.
The transition line (m=0) will move to the left to lower velocities when increasing the external potential, and the opposite if the potential is decreased.
Helium 3-Deuterium Fusion: Negative Mass by Applying an External Electric Field
The net force for Helium 3-Deuterium nuclei during the fusion process was derived in Part 3 and given by Eq. (22):
F_{He3-D}=-\frac{2kq^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{2kq^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}After a little algebra, the simplified version of this fusion net force becomes:
F_{He3-\mathrm{D}}=-\frac{2kq^2}{r^2}+\frac{2kq^2v^2}{r^2c^2}-\frac{4kq^2a}{rc^2} (4)
Assume now that we apply an electric field of magnitude E_f to the “fused” nucleus (Fig. 3), whose net force is given by Eq. (4). The force exerted by this external electric field on the “fused nucleus” is, as usual: F_{ext}=Q\cdot E_f, where “Q” is the net charge of both nuclei.
The net charge for the Helium-3 nucleus is 2p, and for the Deuterium nucleus it is 1p. Then, the total net charge is Q\ =3q\ =3\cdot{1.6\ 10}^{-19}C\ =\ {4.8\ 10}^{-19}C.
Applying Newton’s second law to the system formed by the two “fusing” nuclei, we have:
\sum F=m_{sys}\cdot a=F_{He3-\mathrm{D}}+F_{ext};
m_{sys}=\frac{1}{a}\cdot\left(F_{He3-\mathrm{D}}+F_{ext}\right)After replacing the two forces and the net charge “Q” of both nuclei, the mass equation becomes:
m_{sys}=\frac{1}{a}\cdot\left(-\frac{2kq^2}{r^2}+\frac{2kq^2v^2}{r^2c^2}-\frac{4kq^2a}{rc^2}+3q\cdot E_f\right) (5)
Since the electric field is caused by an external electric potential V_f, this potential applied across the “fusing” nuclei is: V_f=E_f\cdot\left(2r_n\right), where 2r_n is the diameter of the fused nucleus. Now we can replace the electric field in Eq. (5), which gives us the final equation of the system mass:
m_{sys}=\frac{1}{a}\cdot\left(-\frac{2kq^2}{r^2}+\frac{2kq^2v^2}{r^2c^2}-\frac{4kq^2a}{rc^2}+3q\cdot\frac{V_f}{2r_n}\right) (6)
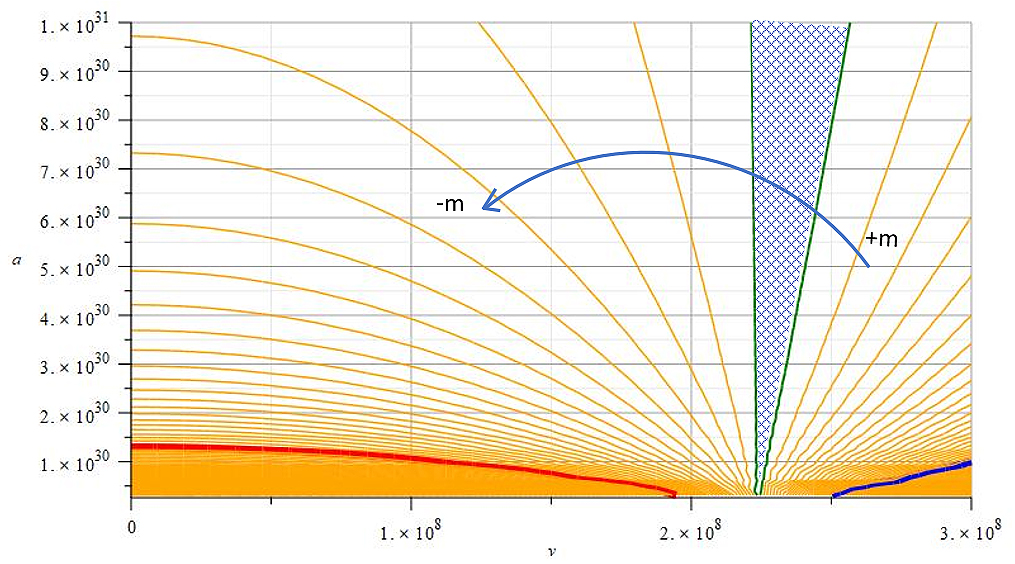
Graph of mass vs. velocity and acceleration showing the regions of negative mass and positive mass and the transition zone for Helium3-Deuterium fusion
The distance between charge centers for the released energy of the fusion was calculated during the analysis of the Helium3-Deuterium fusion made in Part 3, which resulted in r=0.156\ {10}^{-15}m. It seems somewhat logical that we use this value in Eq. (6). The average nucleus radius for Helium-3 and Deuterium is very similar and taken as r_n=2\ {10}^{-15}m.
Figure 5 shows a level or contour graph of Eq. (6) for the system mass of the Helium-3 and Deuterium nuclei with respect to the relative velocity and acceleration, for the following parameters: r=0.156\ {10}^{-15}m, r_n=2\ {10}^{-15}m and V_f=70\ {10}^6V.
As a reference, the masses of the Helium-3 and Deuterium nuclei, when added, give a total mass of m=8.35\ {10}^{-27}Kg.
The thick blue line corresponds to a mass value m=8.41\ {10}^{-27}Kg, while the mass corresponding to the thick red line is m=-8.23\ {10}^{-27}Kg.
In the blue-shaded area between the two green lines lies the m=0 vertical line, which gives the transition between positive and negative mass regions. To avoid “lines’ jam” in the plot, only a few level lines are shown. The mass corresponding to the right green line is m=2.69\ {10}^{-28}Kg, while the mass given by the left green line is m=-8.53\ {10}^{-29}Kg.
The transition line (m=0) will move to the left to lower velocities when increasing the external potential, and the opposite if the potential is decreased.
Possible Additional Reactions in D-T and He3-D Fusion with Negative Mass
In Part 3 we have analyzed in detail the Deuterium-Tritium fusion as well as the Helium3-Deuterium fusion. Both fusions generate specific products and a certain amount of released energy under normal circumstances.
However, under a negative mass regime, more reactions will take place due to the attractive force between charges of the same sign. The electron-proton pair that makes the “neutron” will totally unbind when outside the nucleus during its decay process, which now will happen faster than normal because of the high external potential applied to the system.
Under such circumstances, the formula used to balance the number of neutrons and protons becomes useless. The possible reactions are given by the balance of charges instead.
Now, both the D-T and He3-D fusions will take place in the same system.
How to Calculate New Possible Reactions
As an example, let’s look at the reaction of Helium-4 with a proton, which may give two different products (remember that 1n = 1e+1p).
- \left(4p+2e\right)+1p\rightarrow\left(3p+2e\right)+2p (He4+1p\ \rightarrow\ H3+2p)
- \left(4p+2e\right)+1p\rightarrow\left(3p+1e\right)+\left(2p+1e\right) (He4+1p\ \ \rightarrow\ He3+H2)
Possible Additional Reactions that Take Energy from the System
1) The two reactions of the alpha particle with a proton:
He4+1p\rightarrow H3+2p => Q=-19.8\ MeV
Tritium is radioactive, with a normal half-life of around 12 years. It will decay into Helium-3 by beta minus decay: H3\rightarrow He3+e^-+\overline{\nu} => (Q=18.8\ KeV).
The second reaction:
He4+1p\rightarrow He3+H2 => Q=-18.3\ MeV
2) If a Neutron (still electron-proton bound) collides with Helium-4:
He4+1n\rightarrow He3+H2+e^-+\left(X,\gamma\right) => Q=-18.1\ MeV
3) A positron colliding with Helium-4:
e^++He4\rightarrow He3+1p+\left(X,\gamma\right) => Q=-19.3\ MeV
4) If one proton collides with Helium-3:
1p+He3\rightarrow H2+2p+\left(X,\gamma\right) => Q=-5.5\ MeV
Possible Additional Reactions that Generate Energy
5) Reaction D-D may also happen:
H2+H2\rightarrow H3+1p => Q=4\ MeV
Tritium is radioactive, with a normal half-life of around 12 years. It will decay into Helium-3 by beta minus decay: H3\rightarrow He3+e^-+\overline{\nu} => (Q=18.8\ KeV).
6) If two protons collide with a still unbound Neutron:
2p+1n\rightarrow He3+\left(X,\gamma\right) => Q=7.7\ MeV
7) If one proton collides with a still unbound Neutron:
1p+1n\rightarrow H2+\left(X,\gamma\right) => Q=2.2\ MeV
8) If one proton collides with a Deuterium nucleus:
1p+H2\rightarrow He3+\left(X,\gamma\right) => Q=5.5\ MeV
9) If a Neutron (still electron-proton bound) collides with a Deuterium nucleus:
1n+H2\rightarrow H3 => Q=6.2\ MeV
Tritium is radioactive, with a normal half-life of around 12 years. It will decay into Helium-3 by beta minus decay: H3\rightarrow He3+e^-+\overline{\nu} => (Q=18.8\ KeV).
10) If two protons collide with a Deuterium nucleus:
2p+H2\rightarrow He3+1p+\left(X,\gamma\right) => Q=5.5\ MeV
11) If two protons collide:
1p+1p\rightarrow H2+e^++\nu => Q=1.4\ MeV
12) If a positron collides with a Tritium nucleus:
e^++H3\rightarrow He3\cdot+\left(X,\gamma\right) => Q=0.5\ MeV
13) If two electrons collide:
e^-+e^-\rightarrow\left(X,\gamma\right) => Q=0.51\ MeV
Net Energy production in D-T and He3-D Fusion by considering all possible reactions
The energy generated by the two main reactions, D-T and He3-D (Q=35.9\ MeV) plus the possible reactions that generate energy (Q=33.7\ MeV) gives a total generated energy of: Q=69.6\ MeV
The two reactions in 1) will likely not happen simultaneously. So, let’s take the one that requires more energy as the valid one. Thus, the energy taken from the system will be: Q=-62.6\ MeV.
The net energy is:
Q_{net}=69.6\ MeV-62.6\ MeV=\ 7\ MeVHowever, if the neutron is unbound very fast into an electron and proton, the reaction 2) will never happen. In this case, the net energy generated by the system becomes:
Q_{net}=25.1\ MeV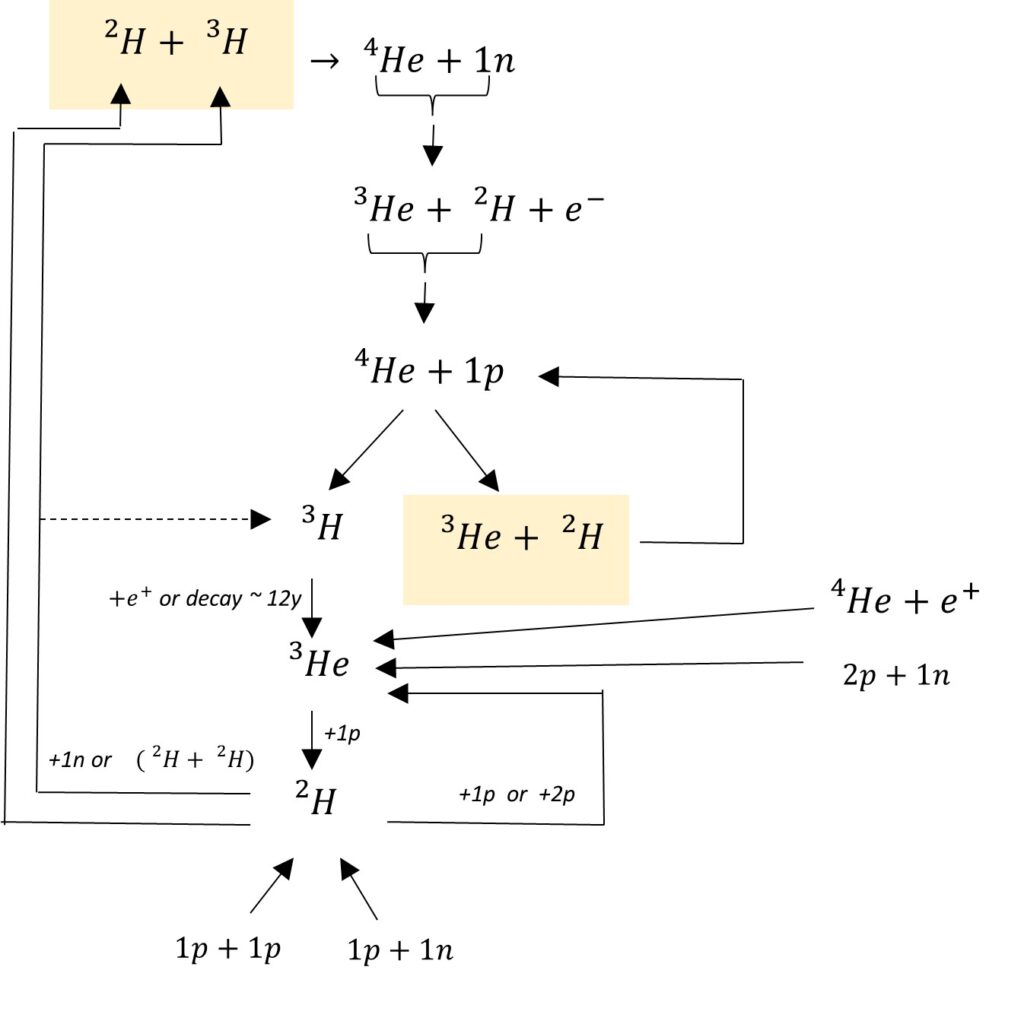
Possible Additional Reactions in D-T and He3-D Fusion with Negative Mass
Figure 6 shows the main reactions as well as some of the possible reactions that may happen in the system.
Note how the system might produce its own fuel to keep reactions happening.
It seems that negative mass fusion might create a kind of feedback that triggers and sustains the reactions in the system.
We have seen in previous paragraphs that the reactions that produce fuel take energy from the system. On the other hand, we have reactions that generate energy.
If the average net energy is positive, some reactions will take place, and the system will keep running. If the energy balance is negative at some point, then no fusion will occur.
Bear in mind that this is a theoretical approach that must be validated by experiments.
Possible Additional Reactions in Tritium-Tritium Fusion with Negative Mass
You may want to check the regular reactions that are described in Part 3.
The electron-proton pair that makes the “neutron” will totally unbind when outside the nucleus during its decay process, which now will happen faster than normal because of the high external potential applied to the system.
Under such circumstances, the formula used to balance the number of neutrons and protons becomes useless. Now the possible reactions are given by the balance of charges instead.
1) H3+H3\rightarrow He4+2n => Q=11.3\ MeV
2) H3+H3\rightarrow H2+He4+1e => Q=13.8\ MeV
3) H3+H3\rightarrow H2+He3+1n+1e => Q=-6.7\ MeV
4) H3+H3\rightarrow H2+H2+2n => Q=-12.5\ MeV
The energy balance of all four reactions, if they happen to occur the same number of times each, will be:
Q_{net}=5.9\ MeVPossible Additional Reactions in Helium3-Helium3 Fusion with Negative Mass
You may want to check the regular reactions that are described in Part 3.
The electron-proton pair that makes the “neutron” will totally unbind when outside the nucleus during its decay process, which now will happen faster than normal because of the high external potential applied to the system.
Under such circumstances, the formula used to balance the number of neutrons and protons becomes useless. Now the possible reactions are given by the balance of charges instead.
1) He3+He3\rightarrow H2+1n+3p => Q=-13.2\ MeV
2) He3+He3\rightarrow H3+3p => Q=-6.9\ MeV
3) He3+He3\rightarrow He4+2p => Q=12.8\ MeV
The energy balance of all four reactions, if they happen to occur the same number of times each, will be:
Q_{net}=-7.3\ MeVPossible Additional Reactions in Helium4-Helium4 Fusion with Negative Mass
Since this possible fusion is an interesting case, both the regular and additional reactions were described in detail in Part 3.
None of these reactions are useful because almost all of them take huge quantities of energy from the system.
Due to the very large amount of energy needed for these reactions to happen, they may only take place in some stars that can eventually supply such energy. Otherwise, they will never happen.
Proposed Device for Negative Mass Nuclear Fusion
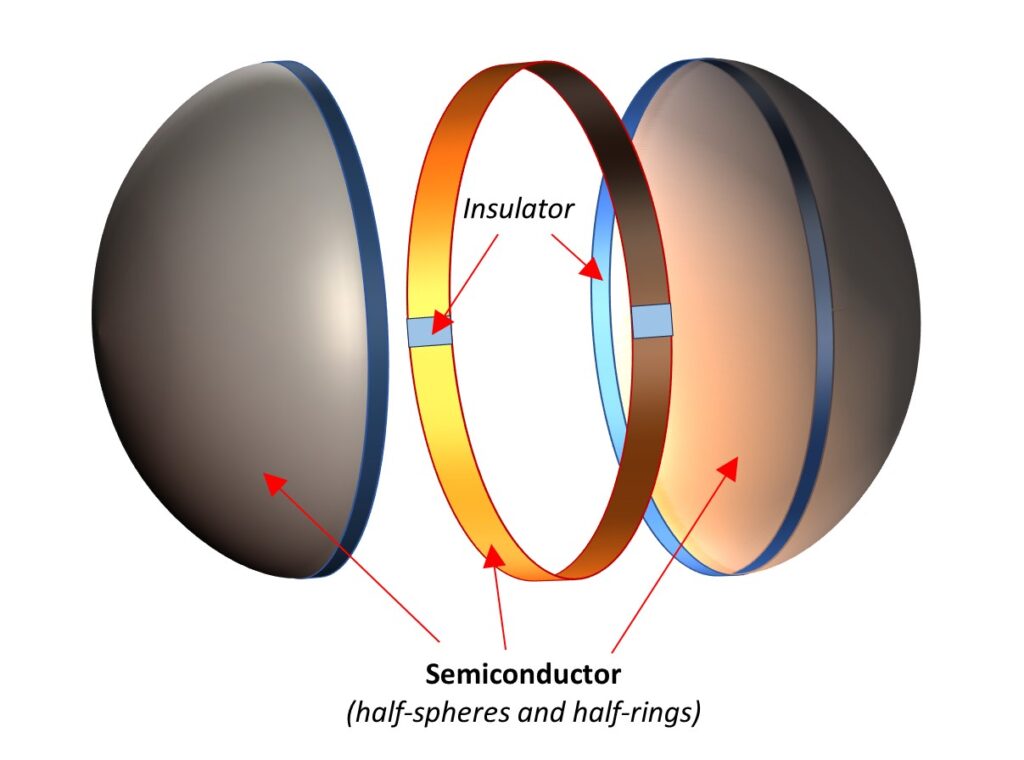
Basic parts of the negative mass nuclear fusion cell
The basic idea to take advantage of the negative mass fusion is to make the reactions inside a water capacitor, which will be called a “negative mass nuclear fusion cell”. To make the reactants behave as if they have a negative effective mass, the capacitor should be connected to a high voltage.
The principal parts of the capacitor are shown in Fig. 7. The capacitor plates are two spherical caps of semiconductor material of the proper type and doping, which are duly isolated in the junction.
The inner part of the junction of the two caps is covered by two half-rings of semiconductor material of the proper type and doping, separated by insulators if necessary.
The negative mass nuclear cell capacitor will be filled with sea water or “heavy water” to provide a basic reactant such as Deuterium (see Fig. 8). In the negative mass regime, other reactants will be produced inside the capacitor.
The two semiconductor caps, besides providing high voltage to the system, will also serve to harvest charges and radiation for the generation of electricity [9]. The semiconductor half-rings inside the cap’s junction are not connected to high voltage. They will merely act as “collectors” of charges and radiation to help in the generation of electricity. The half-rings may also minimize possible radiation leakage through the caps’ insulator.
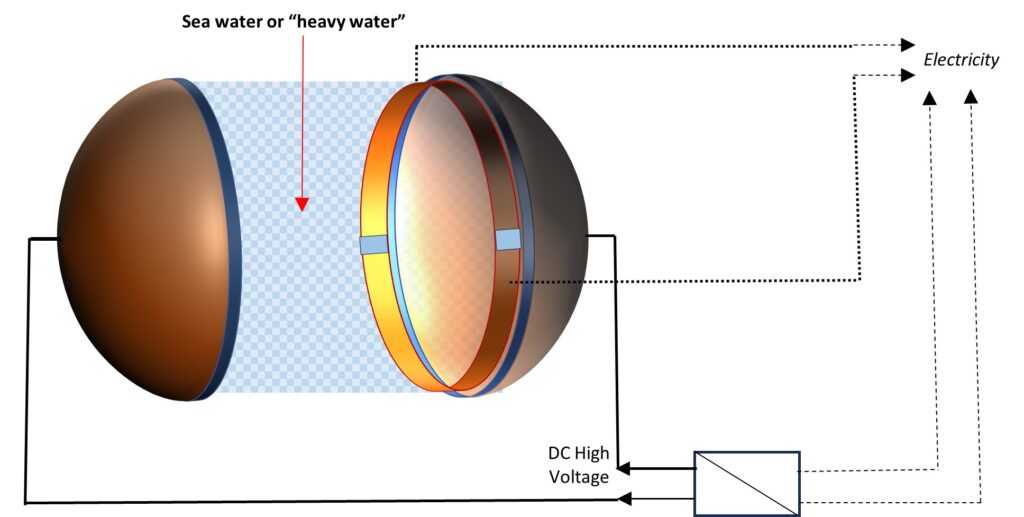
Basic assembling and connections of the negative mass nuclear fusion cell
The spherical shape of the caps may serve three purposes.
First, they will harvest charges and radiation and convert them all into electricity.
Secondly, they will cause a great number of reflections and absorptions of the radiation inside the device, thus minimizing the possible leakage of high energy radiation.
Third, they will make the electric field focalized in the central region of the device, creating a variable electric flux in function of the distance to the caps.

The negative mass nuclear fusion cell assembled and filled with sea water or heavy water
A basic assembly and connection are shown in Fig. 8, while Fig. 9 shows the negative mass nuclear fusion cell fully assembled and filled with sea water or heavy water.
This is not, by any means, equipment meant to guarantee the operation of a negative mass nuclear fusion device.
This is merely a basic concept for a system that could be used to achieve all the benefits associated with negative mass nuclear fusion.
If experiments validate the negative mass nuclear fusion cell, the device might be connected in parallel or in series to generate the required energy for a particular need.
The electrical breakdown of water is much smaller than that of the semiconductor and will ultimately determine the smallest size of the cell. It is necessary to conduct experiments to ascertain whether the electric field between the plates (spherical caps) should be pulsed with a specific duty cycle and PRF or kept constant. Remember that the electric breakdown in each scenario will be unique. One possible minimum cell size estimate is about 70 cm.
In order to enhance the electrical breakdown in the water without affecting the fusion process, chemists could identify which substances should be added. That’s how you get the cell as small as it can get. The thickness of the semiconductor should not only withstand the electrical breakdown, but most importantly, it must absorb 100% of the most powerful gamma radiation to convert it into electricity, thereby avoiding any radiation leakage outside the cell.
This cell (or cells) could be used to power whatever you want, such as appliances, computers, cars, houses, buildings, factories, airplanes, ships, trains, etc. Power plants should not be necessary anymore. The energy transported by cables should disappear.
The study developed in this series of papers is only a theory that predicts how nuclear fusion can be improved with negative mass.
Experiments are needed to validate any theory. And to make things happen.
Conclusions
The attraction force between charges of the same sign in a negative mass regime has been clearly stated.
It was demonstrated that negative mass nuclear fusion has several advantages compared to current projects around the world.
The mass behavior of the reactants of important nuclear fusions has been thoroughly analyzed, and the negative mass operating region has been comprehensively shown.
Besides the main fusion reactions, new, additional reactions were calculated under a negative mass regime that might increase the “standard” released energy.
A device named “negative mass nuclear fusion cell” was proposed to make fusion under a negative mass regime. It could be a simple and cheap alternative to generate electricity.
Bibliography
[1]. Raul Fattore, “Negative Mass and Negative Refractive Index in Atom Nuclei – Nuclear Wave Equation – Gravitational and Inertial Control” (2023), Part-1, Part-2, Part-3, Part-4, Part-5, Part-6
[2]. Raul Fattore, “What is Charge? – The Redefinition of Atom – Energy to Matter Conversion” (2023), https://physics-answers.com/what-is-charge-the-redefinition-of-atom-energy-to-matter-conversion/
[3]. David L. Bergman, “Shape & Size of Electron, Proton & Neutron” (2004), Foundations of Science
[4]. N. Graneau, T. Phipps Jr, and D. Roscoe, “An experimental confirmation of longitudinal electrodynamic forces” (2001), The European Physical Journal, https://www.researchgate.net/publication/225353333_An_experimental_confirmation_of_longitudinal_electrodynamic_forces
[5]. V. Milián-Sánchez, F. Scholkmann, et al., “Fluctuations in measured radioactive decay rates inside a modified Faraday cage: Correlations with space weather” (2020), Nature, https://www.nature.com/articles/s41598-020-64497-0
[6]. J.M. Mack, et al., “Remarks on detecting high-energy deuterium–tritium fusion gamma rays using a gas Cherenkov detector” (2006), Los Alamos National Laboratory, Lawrence Livermore National Laboratory, https://www.sciencedirect.com/science/article/abs/pii/S0969806X05003683
[7]. G.R. Mackenzie, et al., “A diamond gammavoltaic cell utilizing surface conductivity and its response to different photon interaction mechanisms” (2021), School of Physics, University of Bristol, https://www.sciencedirect.com/science/article/abs/pii/S2468606921000538
[8]. M. G. Spencer, T. Alam, “High power direct energy conversion by nuclear batteries” (2019), Applied Physics Reviews. 6. 031305. 10.1063/1.5123163, https://www.researchgate.net/publication/335809562_High_power_direct_energy_conversion_by_nuclear_batteries
[9]. K. Hashizume, et al., “Direct Energy Conversion from Gamma Ray to Electricity Using Silicon Semiconductor Cells” (2010), MRS Online Proceeding Library Archive. 1264. 1264-BB05. 10.1557/PROC-1264-BB05-01, https://www.researchgate.net/publication/330650579_Direct_Energy_Conversion_From_Gamma_Ray_to_Electricity_Using_Silicon_Semiconductor_Cells
[10]. Nie Luo, et al., “Proton bremsstrahlung and its radiation effects in fusion reactors” (2010), Department of Nuclear, Plasma and Radiological Engineeing, Univerisity of Illinois, https://www.sciencedirect.com/science/article/abs/pii/S0920379609002440
[11]. INTERNATIONAL ATOMIC ENERGY AGENCY, Fusion Physics, Non-serial Publications, IAEA, Vienna (2012), https://www.iaea.org/publications/8879/fusion-physics
Related articles:
Nuclear Fusion Enhanced by Negative Mass – A Proposed Method and Device – (Part 1)
Nuclear Fusion Enhanced by Negative Mass – A Proposed Method and Device – (Part 2)
Nuclear Fusion Enhanced by Negative Mass – A Proposed Method and Device – (Part 3)
What is Charge? – The Redefinition of Atom – Energy to Matter Conversion
Charge Radiation Derived from the Universal Electrodynamic Force – Proof of the Cherenkov Effect
Faster-Than-Light Travel Feasible with Negative Mass – Superluminal Dynamics
New Atomic Model with Real-Valued Wave Function – Energy Levels, Spectrum, and Atomic Fine Structure
