Raul Fattore
May 27, 2024
This study is divided into four parts
Table of Contents
Summary of Part 3
A method for modifying particle decay rate is proposed, potentially enabling charge harvesting. Nuclear structure and total energy calculations for various nuclei are demonstrated, revealing the “neutron” as an electron-proton bound in some fusion calculations. Deficient results from Classical Mechanics and Einstein’s mass defect/excess calculation are emphasized, along with the risks associated with insufficient energy calculations. Real released energy and single product energy, including radiation energy, are calculated, and the real energy amount released in a fusion matches the total energy equation from the Universal Electrodynamic Force.
Abstract
The increasing need for energy by mankind over time has led to climate change problems and, most importantly, human health issues due to the storage of radioactive waste that lasts a very long time, thus affecting future generations.
Advances in atomic and nuclear physics several years ago promised a revolution in energy production, offering a significant advantage over burning coal, gas, or oil. Unfortunately, scientists at that time did not make use of their brains appropriately. They simply misused and wasted all the advanced knowledge acquired in atomic and nuclear physics to just boil water!
Nuclear fusion was “reborn” as an alternative to generate energy that might be “clean” for the environment, with “minimum” radiation risks for mankind and no radioactive waste. Clean energy generation and radiation-free risks can only be guaranteed by using certain technology for nuclear fusion.
Making a fusion reaction happen is not complicated (like 14-year-old Taylor Wilson did in his home in 2008). However, there are two main problems with nuclear fusion that have prevented it from being commercially viable until now:
- Efficiency
- Safety
Currently, most scientists experimenting with nuclear fusion are making serious mistakes. They are using costly devices and wasting vast amounts of energy in an attempt to replicate conditions found in stars on Earth, with no encouraging outcomes to date. Why? Fusions in stars are processes that are fully determined by probability, so you cannot build a project just on them. Probability is not the same as certainty, even when it represents the likelihood that an event will occur.
Negative mass calculations can provide certainty regarding an effective head-on collision of charges, but scattering cross-section calculations cannot.
Nuclear fusion can be greatly eased by negative mass. I refer the reader to the series of articles about Negative Mass in Atom Nuclei [1] to understand how we can have negative mass behavior in nuclei.
- Is nuclear fusion enhanced with negative mass nuclei and particles?
- Can negative mass nuclear fusion be made efficient?
- Can negative mass nuclear fusion offer better safety?
- Does negative mass nuclear fusion rely on statistical processes?
- Does negative mass nuclear fusion offer a simpler and cheaper method to generate energy?
In the development of this study, you’ll find comprehensible answers to the above questions, which are backed by the experimentally proven laws of electrodynamics through the Universal Electrodynamic Force and the New Atomic Model.
Introduction
Nuclear fusion is an extremely fast and violent event that involves the acceleration of charges, whether they are nuclei or single charges. Therefore, scientists should not lose sight of the fact that in any atomic and nuclear interaction, we are dealing with accelerated electric charges.
As such, radiation is always present in any nuclear fusion reaction. No exception.
Due to the huge acceleration of the charges, the spectrum may easily range from X-rays to the most powerful gamma radiation. This radiation can be used in our favor to generate electric energy [9]. However, if this radiation is not properly handled, it will be harmful for human health.
For simplicity, the radiation symbols will be omitted in most of the reaction calculations throughout this study. However, as radiation is always present in any nuclear fusion, from X-ray to gamma, the right way to write a reaction should be to include the radiation symbols as part of the fusion products: A+B\ \rightarrow\ C+D\ +\ \left(X,\ \gamma\right).
Unfortunately, scientists are making deficient calculations of the released energy during nuclear fusion. Why?
Because they use wrong formulas that don’t give the total energy of the system, like the known Einstein’s formula E=\Delta m\ c^2 for mass excess/defect calculations. This formula only gives a result for rest mass energy (potential energy), which should be equivalent to the acquired kinetic energy, but it gives no clues about acceleration. The Einstein energy formula is flawed even in its “relativistic” form since, as in classical mechanics, acceleration is entirely disregarded.
The total energy in a fusion reaction is always higher than the results given by Einstein’s formulas for rest energy and the calculations of kinetic energy from classical mechanics.
Most of the energy values for nuclear fusion given in the scientific literature are deficient because none of them consider radiation energy, which on occasion may be much higher than kinetic energy alone.
Applying Einstein’s formulas and classical mechanics’ kinetic energy calculations to nuclear fusion is extremely risky, since you can never be certain of the amount of radiation generated during a reaction.
The scientific community must be aware when using those formulas because:
• They only give partial energy values.
• They are not compatible with a system of charges.
Those formulas may only be applied to limited, simple mechanical interactions between uncharged bodies.
The derivation of the total energy for a system of charges made in this study will provide scientists with a powerful formula to make real energy calculations in any nuclear fusion reaction and many other applications that involve the interaction of charges.
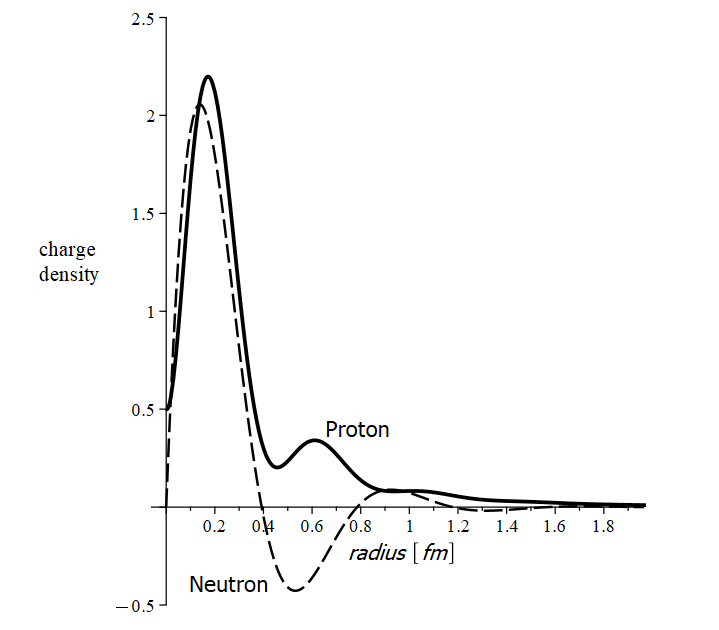
Charge density of the proton and neutron
There are no “neutral particles”. The so-called “neutral particles” are composed of charges that balance the net result [2]. An example of such a particle is the neutron.
Neutrons are stable in the nucleus. However, outside the nucleus, the neutron decays into a proton and an electron with a half-life of fewer than 15 minutes. The mass of the neutron is the sum of the masses of the electron and proton. The neutron has a charge density that varies between positive and negative with respect to its radius (Fig. 1). These facts suggest that the neutron might not be a valid elementary particle but a bound combination of an electron and a proton [3].
Accordingly, the new atomic model precisely describes how electrons and protons are very tightly packed in shells in the nucleus due to the balance of electromagnetic forces.
Based on the energy calculations I made for the Deuterium-Tritium fusion, the binding energy (potential energy) of the electron-proton pair that makes the neutron should be E=-2.127\ MeV when in the nucleus. Outside the nucleus, this energy is given off (radiation, kinetic) during neutron decay time, which unbinds the electron-proton pair.
Because the neutron is always regarded as a “neutral” particle, scientists’ calculations of nuclear reactions and stray reactions may only be partially accurate. The electron and proton may take part in reactions with nuclei or with other electrons and protons when the electron-proton pair that built the neutron unbinds. While some of these reactions will produce energy, others may use some of the system’s energy to generate the fuel for fusion.
As far as I know, these “additional” reactions were never mentioned in any scientific paper. However, some of them could be of such importance that they cannot be ignored and must be considered in calculations, as will be demonstrated in the development of this study.
Since the neutron is one of the fusion products in several reactions and usually carries a high level of kinetic energy and radiation energy, we might be able to use these facts and the internal structure of the neutron in our favor.
The fact that the neutron is a composite of two charges means that we may expect a radiation spectrum from X-rays to gamma rays when the particle is in positive or negative accelerated motion. This is additional energy that we may harvest from the “neutron”, which can be converted into electricity, besides the charges themselves.
Total Energy of the Neutron as a Proton-Electron Bound
In the series of articles about Negative Mass in Atom Nuclei [1] it is shown how this proton-electron bound is organized in the nucleus in extremely tightly packed shells that are balanced by electrodynamic forces. It was also demonstrated that the main force keeping that nuclear structure so strong is the electrostatic force, while the weaker magnetic forces also contribute to maintaining the nuclear dynamic equilibrium. We also stated that the charges shrink heavily under such extreme forces because they must fit into the extremely short distance among them.
The binding energy or potential energy of the “neutron” (electron-proton pair) in the nucleus should be approximately E=-2.127\ MeV\ =\ -3.40783\ {10}^{-13}\ Joules. This amount of energy is the initial energy of the “neutron” when starting its decay process outside the nucleus.
The Universal Force for the electron-proton pair (neutron) in a head-on collision condition is given by:
F_N=-\frac{k\ q^2\left(\left(1-\frac{v^2}{c^2}\right)r-\frac{2r^2a}{c^2}\right)}{r^3}+\frac{k\ q^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}-\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}+\frac{r^4a}{c^2}\right)}{r^5} (1a)
The binding energy, or potential energy, is normally calculated for zero velocity and acceleration (or at least very low kinetic values). Under such conditions, let’s calculate the distance between the charge centers of the electron-proton pair for the given binding energy.
Recall that the total energy is calculated as follows:
E=-\int_{{10}^{27}}^{r}{F_N\ dr}The binding energy of the “neutron” in Joules is \ E=\ -3.40783\ {10}^{-13}\ [Joules]. Now we can proceed with the integration and solve for r.
-3.40783\ {10}^{-13}=-\int_{{10}^{27}}^{r}{F_N\ dr}As a result, the calculated distance between the charge centers of the electron-proton pair (neutron), is r={0.6753\ 10}^{-15}m.
Now we can calculate the total energy of the “neutron” inside the nucleus, and immediately at the beginning of its decay:
E_N=-\int_{{10}^{27}}^{{0.6753\ 10}^{-15}}F_NdrE_N=-3.408026062\times{10}^{-13}+4.966056036\times{10}^{-43}a+3.786695625\times{10}^{-30}v^2 (1b)
Radioactive Decay Rates can be Modified
There is no reason to believe that the decay rate is immune to external agents or that it is the same for diverse environmental conditions [5]. We should keep in sight that we are dealing with charges. As such, their behavior can easily be changed or altered by electric potentials, electromagnetic fields, and the presence of other charges nearby.
We don’t know if we are able to stop decaying at all. Experiments will give the answer.
But for sure, the decay rate, half-life time, etc., could be adapted to our necessities by using an adequate external agent.
The high binding energy of the electron-proton pair (“neutron”), once outside the nucleus, can be greatly reduced by applying a strong electric field generated by an external potential. The energetic “neutron” will give off energy (radiation, kinetic) more quickly than in its usual decay rate, until the binding energy of the electron-proton pair eventually comes to a value of E=-13.6\ eV, which is the binding energy of the Hydrogen atom.
However, due to the strong electric field, the “neutron” will never reach the conditions to remain as a Hydrogen atom because the electron-proton pair will be stripped apart by the external potential.
At this point, we have captured two useful charges, plus the radiation they have emitted in the process, and converted everything into electricity [9].
We see that the otherwise declared “dangerous” neutron in many scientific papers, could be of invaluable help when it is adequately managed. We may extract good amounts of energy from it that we may use better than just boiling water.
Please note that the same criteria can also be applied to the decay of Tritium.
Deuterium: Nuclear Structure, Total Energy, and Deuterium-Deuterium Fusion
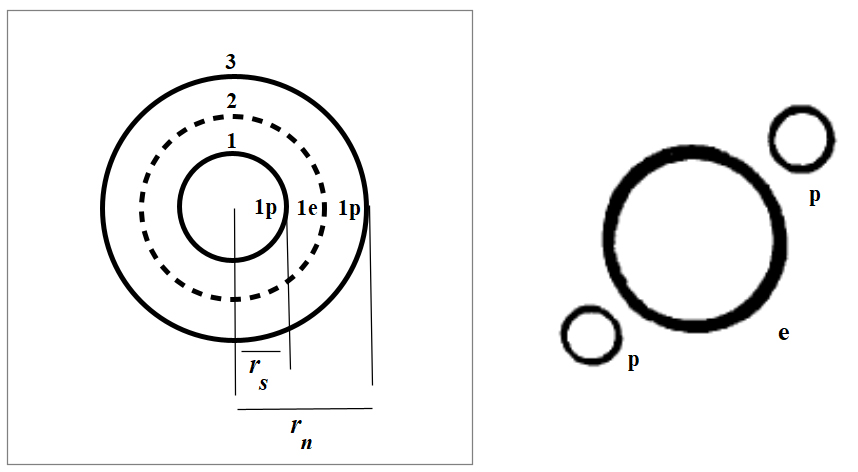
Nuclear structure of Deuterium
Nuclear Structure of Deuterium
In Fig. 2, we see the nuclear structure of Deuterium as shells and the physical orientation of the ring charges according to the New Atomic Model and the Spinning Ring Model of Elementary Particles (a toroidal ring of continuous charge) [1].
The net Force is the sum of the interactions of a shell with all the others. Therefore, the combination of all cross products between two shells will result in a net force of three terms. So, we’ll have 1-2, 1-3 and 2-3 shell interactions, i.e., p-e, p-p, and e-p.
If the charges assemble in rectilinear motion, the Universal Force is:
\vec{F_u}=\left(\frac{kq_1q_2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}-\frac{kq_1q_2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}\right)\hat{r} (1)
The three interaction forces, each with the proper sign of the charges, are:
F_1=\left(\frac{-k\cdot q^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{k\cdot q^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}\right)\ \ \ \ \ \ p-e\ interaction;
F_2=\left(\frac{k\cdot q^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}-\frac{k\cdot q^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}\right)\ \ \ \ p-p\ interaction;
F_3=\left(\frac{-k\cdot q^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{k\cdot q^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}\right)\ \ \ \ \ e-p\ interactionThe addition of the three forces above will give us the net force in the Deuterium nucleus:
F_D=-\frac{k\ q^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{k\ q^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5} (2)
Total Energy of Deuterium
Nowadays, masses are measured with very high precision and constitute trustworthy values that we may use for very accurate calculations.
One easy way to calculate the rest energy (binding energy or potential energy) is by using the formula that is wrongly named “mass-energy”:
E=\left(m_{nuc}-\left(Z\cdot m_p+N\cdot m_N\right)\right)\cdot c^2\ \ [Joules]Where m_{nuc} is the nuclear mass, m_p the proton mass, m_N the neutron mass, Z the number of protons, N the number of neutrons, and c the speed of light.
For Deuteron:
E_\mathrm{D}=\left({3.343583772410}^{-27}-\left(1\cdot{1.6726219210}^{-27}+1\cdot{1.6749274710}^{-27}\right)\right)\cdot\left({3\ 10}^8\right)^2=-3.569056200\times{10}^{-13}\left[Joules\right]E_\mathrm{D}=-2.227\ MeV (3)
To calculate the average distance between charge centers, we make use of the total energy integral equated to the energy value above, for v = 0, a = 0, and solve for r:
E=-\int_{{10}^{27}}^{r}{F_D\ dr}\ =-3.569056200\times{10}^{-13}\ \ [Joules];
r=0.645\ {10}^{-15}mNow we can obtain the total energy expression for Deuteron. This can be done in two ways: by solving the integral above for the value of r, or by using Eq. (4) from Part-2.
By integration:
E_\mathrm{D}=-\int_{{10}^{27}}^{{0.64572\ 10}^{-15}}F_DdrE_D=-3.564145450\times{10}^{-13}-4.968346791\times{10}^{-43}a+3.960161611\times{10}^{-30}v^2 (4)
By using Eq. (4) from Part 2 and considering that the charges assemble in a head-on collision condition, i.e., \theta=\alpha=\pi:
E=\frac{1}{\sqrt{1+\left(\cos^2{\left(\theta\right)}-1\right)\frac{v^2}{c^2}}}\cdot\left(kq_1q_2\cdot\left(\frac{1}{r_f}-\frac{1}{r_i}\right)-\frac{kq_1q_2}{c^2}\cdot\left(\frac{1}{r_f}-\frac{1}{r_i}\right)\cdot v^2-\frac{2kq_1q_2\cos{\left(\alpha\right)}}{c^2}\cdot\left(\ln{\left(r_i\right)}-\ln{\left(r_f\right)}\right)\cdot a\right)E_D=-3.564145449\times{10}^{-13}+3.960161611\times{10}^{-30}v^2-4.968346791\times{10}^{-43}a (5)
Deuterium-Deuterium Fusion
There are two possible reaction products and energies from the D-D fusion:
{_1^2}H+{_1^2}H\ \rightarrow{_2^3}He+n\ \ \ \ \ \ \ \ Q=3.3\ MeV;
{_1^2}H+{_1^2}H\ \rightarrow{_1^3}H+p\ \ \ \ \ \ \ \ Q=4.03\ MeVLet’s take the second reaction with the highest energy value to calculate the average distance between the charge centers and the total energy of the fusion.
The net force for each Deuterium nucleus is given by Eq. (2). In the fusion process of both nuclei, the net forces will add up to one force. That is, the resultant net force is F_{D-D}=2\ F_D.
F_{D-D}=-\frac{2kq^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{2kq^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5} (6)
As we have already calculated the binding energy of Deuteron in the previous paragraph (Eq. 3), the total energy of the reaction will be twice that energy, that is E_r=2\ E_D=-4.45\ MeV (-{7.1296910}^{-13}\ Joules).
Now let’s find the distance between charge centers for the given reaction energy (for v = 0 and a = 0):
-{7.1296910}^{-13}=-\int_{{10}^{27}}^{r}F_{D-D}dr;
r=0.646\ {10}^{-15}mThen, the total reaction energy of the fusion will be:
E_{DD}=-\int_{{10}^{27}}^{{0.646\ 10}^{-15}}F_{D-D}dr;
E_{DD}=-7.125201238\times{10}^{-13}-9.936649237\times{10}^{-43}a+7.916890265\times{10}^{-30}v^2We can calculate the released energy (E_{rel}) of the reaction as the total energy of the reactants minus the total energy of the products:
E_{rel}=E_r-\left(E_{H1}+E_{H3}\right)Where E_{H1}=0 (proton binding energy), and E_{H3}=-8.48\ MeV (binding energy of Tritium), give us the released energy of the D-D fusion:
E_{rel}=4.03\ MeVHelium 3: Nuclear Structure, Total Energy, and Helium3-Helium3 Fusion
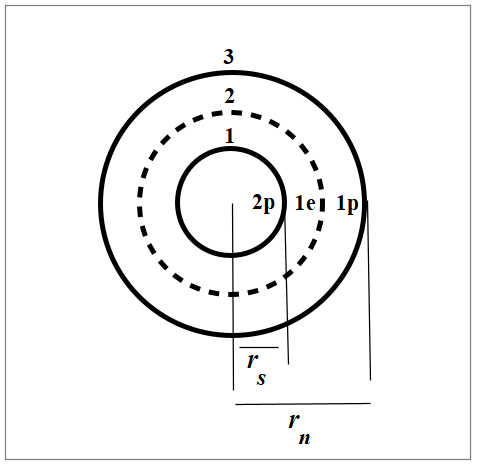
Nuclear structure of Helium 3
Nuclear Structure of Helium 3
In Fig. 3, we see the nuclear structure of Helium 3 in organized shells according to the New Atomic Model and the Spinning Ring Model of Elementary Particles (a toroidal ring of continuous charge) [1].
The net Force is the sum of the interactions of a shell with all the others. Therefore, the combination of all cross products between two shells will result in a net force of three terms. So, we’ll have 1-2, 1-3, and 2-3 shell interactions, i.e., 2p-e, 2p-p, and e-p.
If the charges assemble in rectilinear motion, the Universal Force is given by Eq. (1). The three interaction forces, each with the proper sign of the charges, are:
F_1=2\cdot\left(\frac{-k\cdot q^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{k\cdot q^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}\right)\ \ \ \ 2p-e\ interaction;
F_2=2\cdot\left(\frac{k\cdot q^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}-\frac{k\cdot q^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}\right)\ \ \ \ 2p-p\ interaction;
F_3=\left(\frac{-k\cdot q^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{k\cdot q^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}\right)\ \ \ \ e-p\ interactionThe addition of the three forces above will give us the net force in the Helium 3 nucleus:
F_{He3}=-\frac{kq^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{kq^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5} (7)
Total Energy of Helium 3
Nowadays, masses are measured with very high precision and constitute trustworthy values that we may use for very accurate calculations.
One easy way to calculate the rest energy (binding energy or potential energy) is by using the formula that is wrongly named “mass-energy”:
E=\left(m_{nuc}-\left(Z\cdot m_p+N\cdot m_N\right)\right)\cdot c^2\ \ [Joules]Where m_{nuc} is the nuclear mass, m_p the proton mass, m_N the neutron mass, Z the number of protons, N the number of neutrons, and c the speed of light.
For Helium 3:
E_{He3}=\left({5.00641166448\ 10}^{-27}-\left(2\cdot{1.6726219210}^{-27}+1\cdot{1.6749274710}^{-27}\right)\right)\cdot\left({3\ 10}^8\right)^2=-1.238368140\times{10}^{-12}\ \ JoulesE_{\mathrm{He3}}=-7.73\ MeV (8)
To calculate the average distance between charge centers, we make use of the total energy integral equated to the energy value above, for v = 0, a = 0, and solve for r:
E=-\int_{{10}^{27}}^{r}{F_{He3}\ dr}\ ==-1.238368140\times{10}^{-12}\ \ [Joules];
r=0.186\ {10}^{-15}mNow we can obtain the total energy expression for Helium 3. This can be done in two ways: by solving the integral above for the value of r, or by using Eq. (4) from Part 2.
By integration:
E_{\mathrm{He3}}=-\int_{{10}^{27}}^{{0.186\ 10}^{-15}}F_{He3}drE_{He3}=-1.237333333\times{10}^{-12}-5.032000494\times{10}^{-43}a+1.374814815\times{10}^{-29}v^2 (9)
By using Eq. (4) from Part 2 and considering that the charges assemble in a head-on collision condition, i.e., \theta=\alpha=\pi:
E=\frac{1}{\sqrt{1+\left(\cos^2{\left(\theta\right)}-1\right)\frac{v^2}{c^2}}}\cdot\left(kq_1q_2\cdot\left(\frac{1}{r_f}-\frac{1}{r_i}\right)-\frac{kq_1q_2}{c^2}\cdot\left(\frac{1}{r_f}-\frac{1}{r_i}\right)\cdot v^2-\frac{2kq_1q_2\cos{\left(\alpha\right)}}{c^2}\cdot\left(\ln{\left(r_i\right)}-\ln{\left(r_f\right)}\right)\cdot a\right)E_{He3}=-1.237333333\times{10}^{-12}+1.374814815\times{10}^{-29}v^2-5.032000494\times{10}^{-43}a (10)
Helium 3-Helium 3 Fusion
There might be three possible reactions, namely:
a) {_2^3}He+{_2^3}He\ \rightarrow\ 2\ {_1^3}H+2p\ \ \ \ \ \ Q=-14.6\ MeV
b) {_2^3}He+{_2^3}He\ \rightarrow\ {_1^2}H+{_2^4}He+1p\ \ \ \ \ \ Q=7\ MeV
c) {_2^3}He+{_2^3}He\ \rightarrow\ {_2^4}He+2p\ \ \ \ \ \ Q=12.86\ MeV
For the calculations that follow, we’ll take the reaction products and energies from the He3-He3 fusion c).
Let’s calculate the average distance between the charge centers and the total energy of the fusion.
The net force for each Helium 3 nucleus is given by Eq. (7). In the fusion process of both nuclei, the net forces will add up to one force. That is, the resultant net force is F_{He3-He3}=2\ F_{He3}.
F_{He3-He3}=-\frac{2kq^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{2kq^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5} (11)
As we have already calculated the binding energy of Helium 3 in the previous paragraph (Eq. 8), the total energy of the reaction will be twice that energy, that is E_r=2\ E_{He3}=-15.46\ MeV (-2.476965\ {10}^{-12}\ Joules).
Now let’s find the distance between charge centers for the given reaction energy (for v = 0 and a = 0):
-2.476965\ {10}^{-12}=-\int_{{10}^{27}}^{r}F_{He3-He3}dr;
r=0.186\ {10}^{-15}mThen, the total reaction energy of the fusion will be:
E_{He3-He3}=-\int_{{10}^{27}}^{{0.186\ 10}^{-15}}F_{He3-He3}dr;
E_{He3-He3}=-2.474666667\times{10}^{-12}-1.006400099\times{10}^{-42}a+2.749629630\times{10}^{-29}v^2We can calculate the released energy (E_{rel}) of the reaction as the total energy of the reactants minus the total energy of the products:
E_{rel}=E_r-\left(E_{He4}+2\ E_{H1}\right)Where E_{H1}=0 (proton binding energy), and E_{He4}=-28.3\ MeV (binding energy of Helium-4), give us the released energy of the He3-He3 fusion:
E_{rel}=12.84\ MeVTritium: Nuclear Structure, Total Energy, and Tritium-Tritium Fusion
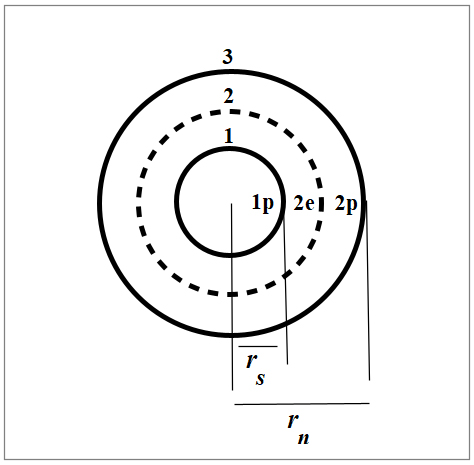
Nuclear structure of Tritium
Nuclear Structure of Tritium
In Fig. 4, we see the nuclear structure of Tritium in organized shells according to the New Atomic Model and the Spinning Ring Model of Elementary Particles (a toroidal ring of continuous charge) [1].
The net Force is the sum of the interactions of a shell with all the others. Therefore, the combination of all cross products between two shells will result in a net force of three terms. So, we’ll have 1-2, 1-3, and 2-3 shell interactions, i.e., p-2e, 1p-2p, and 2e-2p.
If the charges assemble in rectilinear motion, the Universal Force is given by Eq. (1). The three interaction forces, each with the proper sign of the charges, are:
F_1=2\cdot\left(\frac{-k\cdot q^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{k\cdot q^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}\right)\ \ \ \ 1p-2e\ interaction;
F_2=2\cdot\left(\frac{k\cdot q^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}-\frac{k\cdot q^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}\right)\ \ \ \ 1p-2p\ interaction;
F_3=4\cdot\left(\frac{-k\cdot q^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{k\cdot q^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}\right)\ \ \ 2e-2p\ interactionThe addition of the three forces above will give us the net force in the Tritium nucleus:
F_{H3}=-\frac{4kq^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{4kq^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5} (12)
Total Energy of Tritium
Nowadays, masses are measured with very high precision and constitute trustworthy values that we may use for very accurate calculations.
One easy way to calculate the rest energy (binding energy or potential energy) is by using the formula that is wrongly named “mass-energy”:
E=\left(m_{nuc}-\left(Z\cdot m_p+N\cdot m_N\right)\right)\cdot c^2\ \ [Joules]Where m_{nuc} is the nuclear mass, m_p the proton mass, m_N the neutron mass, Z the number of protons, N the number of neutrons, and c the speed of light.
For Tritium:
E_{H3}=\left({5.0073561458110}^{-27}-\left(1\cdot{1.6726219210}^{-27}+2\cdot{1.6749274710}^{-27}\right)\right)\cdot\left({3\ 10}^8\right)^2=-1.360864260\ {10}^{-12}\ \ JoulesE_{\mathrm{H3}}=-8.49\ MeV (13)
To calculate the average distance between charge centers, we make use of the total energy integral equated to the energy value above, for v = 0, a = 0, and solve for r:
E=-\int_{{10}^{27}}^{r}{F_{H3}\ dr}\ ==-1.360864260\ {10}^{-12}\ \ [Joules];
r=0.676\ {10}^{-15}mNow we can obtain the total energy expression for Tritium. This can be done in two ways: by solving the integral above for the value of r, or by using Eq. (4) from Part 2.
By integration:
E_{\mathrm{H3}}=-\int_{{10}^{27}}^{{0.676\ 10}^{-15}}F_{H3}drE_{H3}=-1.361798817\times{10}^{-12}-1.986401220\times{10}^{-42}a+1.513109796\times{10}^{-29}v^2 (14)
By using Eq. (4) from Part-2 and considering that the charges assemble in a head-on collision condition, i.e., \theta=\alpha=\pi. Note that we must match factor 4 as in force (Eq. 12):
E=\frac{1}{\sqrt{1+\left(\cos^2{\left(\theta\right)}-1\right)\frac{v^2}{c^2}}}\cdot4\left(kq_1q_2\cdot\left(\frac{1}{r_f}-\frac{1}{r_i}\right)-\frac{kq_1q_2}{c^2}\cdot\left(\frac{1}{r_f}-\frac{1}{r_i}\right)\cdot v^2-\frac{2kq_1q_2\cos{\left(\alpha\right)}}{c^2}\cdot\left(\ln{\left(r_i\right)}-\ln{\left(r_f\right)}\right)\cdot a\right)E_{H3}=-1.361798817\times{10}^{-12}+1.513109797\times{10}^{-29}v^2-1.986401221\times{10}^{-42}a (15)
Tritium-Tritium Fusion
There are two possible reactions. One that takes energy from the system, and another one that generates energy.
The reaction products and energies from both cases in the H3-H3 fusion are:
{_1^3}H+{_1^3}H\ \rightarrow\ {_2^4}He+2n\ \ \ \ \ \ Q=11.3\ MeV;
{_1^3}H+{_1^3}H\ \rightarrow\ {_1^2}H+{_1^2}H+2n\ \ \ \ \ \ Q=-12.5\ MeVBeing optimistic (though not realistic), we may assume that the system is unable to supply the energy for the second reaction to happen. So, in our example, we’ll work with the first reaction.
Let’s calculate the average distance between the charge centers and the total energy of the fusion.
The net force for each Tritium nucleus is given by Eq. (12). In the fusion process of both nuclei, the net forces will add up to one force. That is, the resultant net force is F_{H3-H3}=2\ F_{H3}.
F_{H3-H3}=-\frac{8kq^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{8kq^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5} (16)
As we have already calculated the binding energy of Tritium in the previous paragraph (Eq. 13), the total energy of the reaction will be twice that energy, that is E_r=2\ E_{H3}=-16.98\ MeV (-2.720496\ {10}^{-12}\ Joules).
Now let’s find the distance between charge centers for the given reaction energy (for v = 0 and a = 0):
-2.720496\ {10}^{-12}=-\int_{{10}^{27}}^{r}F_{H3-H3}dr;
r=0.677\ {10}^{-15}mThen, the total reaction energy of the fusion will be:
E_{H3-H3}=-\int_{{10}^{27}}^{{0.677\ 10}^{-15}}F_{H3-H3}dr;
E_{H3-H3}=-2.719574594\times{10}^{-12}-3.972741960\times{10}^{-42}a+3.021749549\times{10}^{-29}v^2We can calculate the released energy (E_{rel}) of the reaction as the total energy of the reactants minus the total energy of the products. The released energy calculation will depend on how we consider the neutron: as a “neutral” unbound particle, or as an electron-proton bound.
a. Released energy with the neutron as an unbound, “neutral particle”:
E_{rel}=E_r-\left(E_{He4}+0\cdot E_N\right)Where E_{He4}=-28.3\ MeV (binding energy of Helium-4), and E_N=0\ MeV (binding energy of the neutron), give us the released energy of the T-T fusion:
E_{rel}=11.32\ MeVb. Released energy with the neutron as an electron-proton bound:
We assume that the neutron keeps its binding energy immediately after leaving the nucleus, before starting its decay. It means that this released energy will reach its maximum in this instant, and then gradually decrease.
E_{rel}=E_r-\left(E_{He4}+E_N\right)Where E_{He4}=-28.3\ MeV (binding energy of Helium-4), and E_N=-2.127\ MeV (binding energy of the electron-proton that constitutes the “neutron”, immediately after leaving the nucleus). That gives us the released energy of the T-T fusion at the earliest instant:
E_{rel}=13.4\ MeVHelium 4: Nuclear Structure, Total Energy, and Helium4-Helium4 Fusion
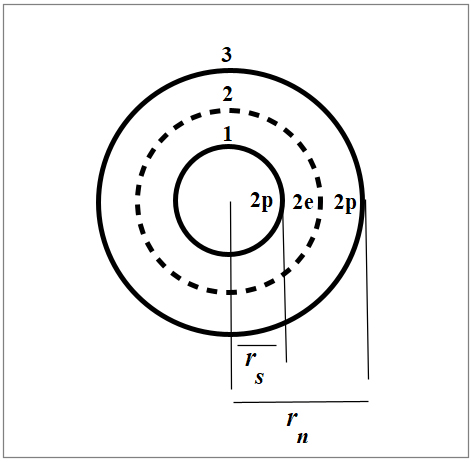
Nuclear structure of Helium 4
Nuclear Structure of Helium 4
In Fig. 5 we see the nuclear structure of Helium 4 in organized shells according to the New Atomic Model and the Spinning Ring Model of Elementary Particles (a toroidal ring of continuous charge) [1].
The net Force is the sum of the interactions of a shell with all the others. Therefore, the combination of all cross products between two shells will result in a net force of three terms. So, we’ll have 1-2, 1-3, and 2-3 shell interactions, i.e., 2p-2e, 2p-2p, and 2e-2p.
If the charges assemble in rectilinear motion, the Universal Force is given by Eq. (1). The three interaction forces, each with the proper sign of the charges, are:
F_1=4\cdot\left(\frac{-k\cdot q^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{k\cdot q^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}\right)\ \ \ \ 2p-2e\ interaction;
F_2=4\cdot\left(\frac{k\cdot q^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}-\frac{k\cdot q^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}\right)\ \ \ 2p-2p\ interaction;
F_3=4\cdot\left(\frac{-k\cdot q^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{k\cdot q^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}\right)\ \ \ 2e-2p\ interactionThe addition of the three forces above will give us the net force in the Helium-4 nucleus:
F_{He4}=-\frac{4kq^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{4kq^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5} (17)
Total Energy of Helium-4
Nowadays, masses are measured with very high precision and constitute trustworthy values that we may use for very accurate calculations.
One easy way to calculate the rest energy (binding energy or potential energy) is by using the formula that is wrongly named “mass-energy”:
E=\left(m_{nuc}-\left(Z\cdot m_p+N\cdot m_N\right)\right)\cdot c^2\ \ [Joules]Where m_{nuc} is the nuclear mass, m_p the proton mass, m_N the neutron mass, Z the number of protons, N the number of neutrons, and c the speed of light.
For Helium-4:
E_{He4}=\left({6.64465675310}^{-27}-\left(2\cdot{1.6726219210}^{-27}+2\cdot{1.6749274710}^{-27}\right)\right)\cdot\left({3\ 10}^8\right)^2=-4.539782430\times{10}^{-12}\ JoulesE_{\mathrm{He4}}=-28.3\ MeV (18)
To calculate the average distance between charge centers, we make use of the total energy integral equated to the energy value above, for v = 0, a = 0, and solve for r:
E=-\int_{{10}^{27}}^{r}{F_{He4}\ dr}\ =-4.539782430\ {10}^{-12}\ \ [Joules];
r=0.203\ {10}^{-15}mNow we can obtain the total energy expression for Helium-4. This can be done in two ways: by solving the integral above for the value of r, or by using Eq. (4) from Part-2.
By integration:
E_{\mathrm{He4}}=-\int_{{10}^{27}}^{{0.203\ 10}^{-15}}F_{He4}drE_{He4}=-4.534857143\times{10}^{-12}-2.011011021\times{10}^{-42}a+5.038730159\times{10}^{-29}v^2 (19)
By using Eq. (4) from Part-2 and considering that the charges assemble in a head-on collision condition, i.e., \theta=\alpha=\pi. Note that we must match factor 4 as in force (Eq. 17):
E=\frac{1}{\sqrt{1+\left(\cos^2{\left(\theta\right)}-1\right)\frac{v^2}{c^2}}}\cdot4\left(kq_1q_2\cdot\left(\frac{1}{r_f}-\frac{1}{r_i}\right)-\frac{kq_1q_2}{c^2}\cdot\left(\frac{1}{r_f}-\frac{1}{r_i}\right)\cdot v^2-\frac{2kq_1q_2\cos{\left(\alpha\right)}}{c^2}\cdot\left(\ln{\left(r_i\right)}-\ln{\left(r_f\right)}\right)\cdot a\right)E_{He4}=-4.534857144\times{10}^{-12}+5.038730160\times{10}^{-29}v^2-2.011011022\times{10}^{-42}a (20)
Helium 4-Helium 4 Fusion
There are several possible reactions, but most of them (if they can happen) will take energy from the system. The reaction products and energies for all possible reactions in the He4-He4 fusion are given below.
- Possible reactions by considering the neutron as a “neutral” electron-proton bound:
This is a highly unstable reaction that takes some energy from the system. Beryllium 8 will decay back into two alpha particles with a half lifetime of approximately {10}^{-16}s.
If another alpha particle can fuse with the beryllium nucleus before it decays, stable carbon is formed along with gamma radiation. This reaction generates energy:
{_4^8}Be+{_2^4}H{e4}\ \rightarrow{_6^{12}}C\ +\gamma\ \ \ \ \ \ Q=7.3\ MeVMore reactions:
{_2^4}H{e4}+{_2^4}H{e4}\ \rightarrow\ {_3^6}Li+{_1^2}H\ \ \ \ \ \ \ Q=-22.4\ MeV;
{_2^4}H{e4}+{_2^4}H{e4}\ \rightarrow\ {_2^3}He+\ {_2^3}He+2n\ \ \ \ \ \ Q=-41.1\ MeV;
{_2^4}H{e4}+{_2^4}H{e4}\ \rightarrow\ 2\ {_1^3}H+\ {_1^2}H+1p\ \ \ \ \ \ Q=-45.5\ MeV;
{_2^4}H{e4}+{_2^4}H{e4}\ \rightarrow2\ {_1^3}H+2p\ \ \ \ \ \ Q=-39.6\ MeV;
{_2^4}H{e4}+{_2^4}H{e4}\ \rightarrow\ {_1^2}H+\ {_1^3}H+{_2^3}H_e\ \ \ \ \ \ Q=-38.2\ MeV- Possible reactions by considering the neutron as an unbound electron-proton pair:
Once the electron-proton pair that makes the neutron is practically unbound, both charges might participate in reactions involving nuclei or other electrons and protons.
He4+He4\rightarrow2H3+2p\ \ \ \ \ \ \ \ \ Q=-39.6\ MeV;
He4+He4\rightarrow H2+H3+He3\ \ \ \ \ \ \ \ \ \ Q=-38.2\ MeV;
He4+He4\rightarrow Be8\ \ \ \ \ \ \ \ \ Q=-0.1\ MeV;
He4+He4\rightarrow H2+L_i\ \ \ \ \ \ \ \ \ Q=-22.4\ MeVThe first three reactions coincide with three of the reactions described in the previous paragraph.
None of the reactions above are useful because almost all of them take huge quantities of energy from the system. Even the second one in a) that generates energy, might never occur. You must be very, very lucky to get that in such a short lifetime of beryllium.
Due to the huge amount of energy needed, the reactions above may only take place at some stars that can supply the necessary energy. Otherwise, they will never happen.
In our example, we’ll work with the first reaction of section a) above, i.e., until the production of Beryllium-8.
Let’s calculate the average distance between the charge centers and the total energy of the fusion for the chosen reaction chain.
The net force for each Helium-4 nucleus is given by Eq. (17). In the fusion process of both nuclei, the net forces will add up to one force. That is, the resultant net force is F_{He4-He4}=2\ F_{He4}.
F_{He4-He4}=-\frac{8kq^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{8kq^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5} (21)
As we have already calculated the binding energy of Helium-4 in the previous paragraph (Eq. 18), the total energy of the reaction will be twice that energy, that is E_r=2\ E_{He4}=-56.6\ MeV (-{9.06832\ 10}^{-12}Joules).
Now let’s find the distance between charge centers for the given reaction energy (for v = 0 and a = 0):
-{9.06832\ 10}^{-12}=-\int_{{10}^{27}}^{r}F_{He4-He4}dr;
r=0.203\ {10}^{-15}mThen, the total reaction energy of the fusion will be:
E_{He4-He4}=-\int_{{10}^{27}}^{{0.203\ 10}^{-15}}F_{He4-He4}dr;
E_{He4-He4}=-9.069714286\times{10}^{-12}-4.022022042\times{10}^{-42}a+1.007746032\times{10}^{-28}v^2We can calculate the released energy (E_{rel}) of the chosen fusion chain as the total energy of the reactants minus the total energy of the products.
E_{rel}=E_r-\left(E_{Be8}\right)Where E_{Be8}=-56.5\ MeV (the binding energy of Beryllium-8), that gives us the released energy of the chosen fusion chain:
E_{rel}=-0.1\ MeVHelium3-Deuterium Fusion
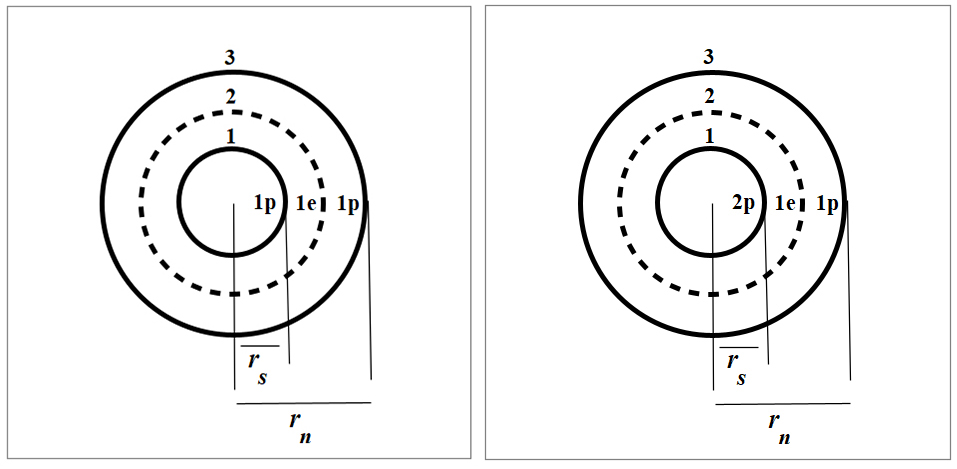
Nuclear structure of Deuterium (left) and Helium-3 (right)
The reaction products and energy of the He3-D fusion are given below.
{_2^3}H_e+{_1^2}H\ \rightarrow\ {_2^4}H_e+1p\ \ \ \ \ \ Q=18.3\ MeVLet’s calculate the average distance between the charge centers and the total energy of the fusion.
The net force for Helium-3 nucleus is given by Eq. (7), while the net force for Deuterium nucleus corresponds to Eq. (2). In the fusion process of both nuclei, the net forces will add up to one force. That is, the resultant net force is F_{He3-D}=F_{He3}+F_D.
F_{He3-D}=-\frac{2kq^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{2kq^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5} (22)
As we have already calculated the binding energies of Helium-3 (Eq. 8) and Deuterium (Eq. 3), the total energy of the reaction will be the sum of both energies, that is E_r=E_{He3}+E_D=-9.96\ MeV (-1.59577\ {10}^{-12}Joules).
Now let’s find the distance between charge centers for the given reaction energy (for v = 0 and a = 0):
-1.59577\ {10}^{-12}=-\int_{{10}^{27}}^{r}F_{He3-D}dr;
r=0.288\ {10}^{-15}mThen, the total reaction energy of the fusion will be:
E_{He3-D}=-\int_{{10}^{27}}^{{0.288\ 10}^{-15}}F_{He3-D}dr;
E_{He3-\mathrm{D}}=-1.598222222\times{10}^{-12}-1.001928004\times{10}^{-42}a+1.775802469\times{10}^{-29}v^2We can calculate the released energy (E_{rel}) of the fusion as the total energy of the reactants minus the total energy of the products.
E_{rel}=E_r-\left(E_{He4}+E_{H1}\right)Where E_{He4}=-28.3\ MeV (binding energy of Helium-4), and E_{H1}=0\ MeV (binding energy of the proton), give us the released energy of the fusion:
E_{rel}=18.34\ MeVNow let’s find the distance between charge centers for the released energy E_{rel} of the reaction (for v = 0 and a = 0):
2.938392\ {10}^{-12}=-\int_{r}^{{10}^{27}}F_{He3-D}dr;
r=0.156\ {10}^{-15}mThen, the total released energy of the fusion will be:
E_{He3-D}=-\int_{{10}^{27}}^{{0.156\ 10}^{-15}}F_{He3-D}drE=2.950564103\times{10}^{-12}+1.008199218\times{10}^{-42}a-3.278404558\times{10}^{-29}v^2 (22a)
Deuterium-Tritium Fusion
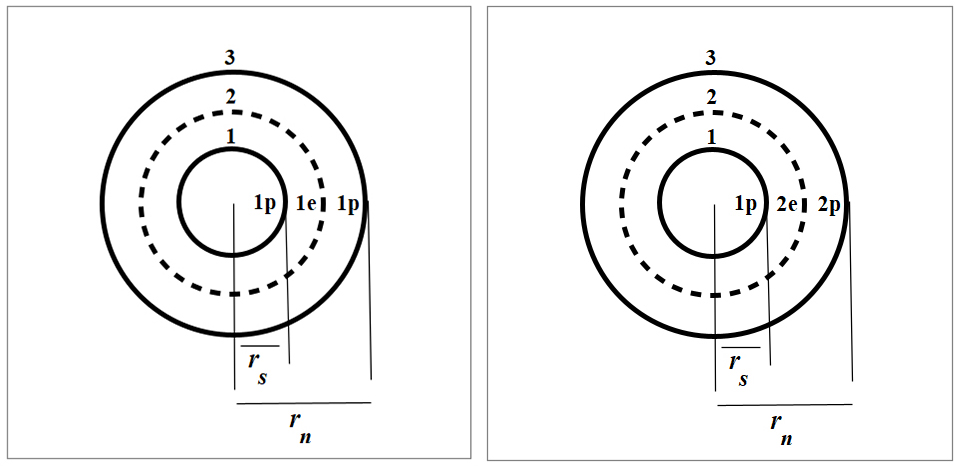
Nuclear structure of Deuterium (left) and Tritium (right)
The reaction products and energy of the D-T fusion are given below.
{_1^2}H+{_1^3}H\ \rightarrow\ {_2^4}H_e+1n\ \ \ \ \ \ Q=17.6\ MeVLet’s calculate the average distance between the charge centers and the total energy of the fusion.
The net force for Tritium nucleus is given by Eq. (12), while the net force for Deuterium nucleus corresponds to Eq. (2). In the fusion process of both nuclei, the net forces will add up to one force. That is, the resultant net force is F_{D-T}=F_D+F_T.
F_{D-T}=-\frac{5kq^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{5kq^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5} (23)
As we have already calculated the binding energies of Tritium (Eq. 13) and Deuterium (Eq. 3), the total energy of the reaction will be the sum of both energies, that is E_r=E_{H3}+E_D=-10.7\ MeV (-{1.71433\ 10}^{-12}Joules).
Now let’s find the distance between charge centers for the given reaction energy (for v = 0 and a = 0):
-{1.71433\ 10}^{-12}=-\int_{{10}^{27}}^{r}F_{D-T}dr;
r=0.671\ {10}^{-15}mThen, the total reaction energy of the fusion will be:
E_{D-T}=-\int_{{10}^{27}}^{{0.671\ 10}^{-15}}F_{D-T}drE_{D-T}=-1.714932936\times{10}^{-12}-2.483191367\times{10}^{-42}a+1.905481040\times{10}^{-29}v^2 (24)
We can calculate the released energy (E_{rel}) of the reaction as the total energy of the reactants minus the total energy of the products. The released energy calculation will depend on how we consider the neutron: as a “neutral” unbound particle, or as an electron-proton bound.
- Released energy with the neutron as an unbound, “neutral particle”:
Where E_{He4}=-28.3\ MeV (binding energy of Helium-4), and E_N=0\ MeV (binding energy of the neutron), give us the released energy of the T-T fusion:
E_{rel}=17.6\ MeV- Released energy with the neutron as an electron-proton bound:
We assume that the neutron keeps its binding energy immediately after leaving the nucleus, before starting its decay. It means that this released energy will reach its maximum in this instant, and then gradually decrease.
E_{rel}=E_r-\left(E_{He4}+E_N\right)Where E_{He4}=-28.3\ MeV (binding energy of Helium-4), and E_N=-2.127\ MeV (binding energy of the electron-proton that constitutes the “neutron”, immediately after leaving the nucleus). That gives us the released energy of the D-T fusion at the earliest instant:
E_{rel}=19.7\ MeVThe Released Energy Calculated with Classical Mechanics
Until now, physicists have been unable to provide a way of calculating the total energy of a dynamic system that, besides velocity, can also account for the acceleration of the particles. You can make kinetic energy calculations based only on the velocity of the particles. But you’ll never know what acceleration was needed to reach that velocity.
Classical Mechanics and the Theory of Relativity are no exceptions, because neither of them provides the right calculation method for the total energy.
Ignoring acceleration in a dynamic system of electric charges will yield totally wrong results. In other words, you are completely dismissing radiation!
That said, let’s make the deficient energy calculations for the fusion products.
We assume that the released energy is given by the addition of the kinetic energy of the products, namely:
E_{rel}=K_{He4}+K_N=2.82\ {10}^{-12}\ Joules\frac{1}{2}m_{He4}v_{He4}^2+\frac{1}{2}m_Nv_N^2={2.82\ 10}^{-12} (24a)
We have one equation with two unknowns (velocities), so we need a second equation to get the velocities. Assuming also that both particles had undergone an elastic collision, the conservation of momentum is given by:
p_{He4}+p_N=0m_{He4}v_{He4}+m_Nv_N=0 (24b)
When solving the system of equations (24a) and (24b) for v_{He4} and v_N, we get: v_{He4}=1.3\ {10}^7\frac{m}{s} and v_N=5.2\ {10}^7\frac{m}{s}.
The kinetic energy of the products is:
K_{He4}=\frac{1}{2}m_{He4}v_{He}^2=5.677695370\times{10}^{-13}\ Joules\ =\ 3.5\ MeV (24c)
K_N=\frac{1}{2}m_Nv_N^2=2.252230463\times{10}^{-12}\ Joules\ =\ 14\ MeV (24d)
By completely ignoring radiation, we finally get the deficient result of the released energy:
E_{rel}=K_{He4}+K_N=17.5\ MeV (24e)
How to Calculate the Real Released Energy and the Single Energy of the Products
So far, we have reviewed several nuclear fusion reactions in previous paragraphs and calculated the released energy in each case.
However, those released energy values are incorrect because they resulted from an inadequate calculation method that completely ignored the radiation energy and relied only on Einstein’s mass excess/defect formula or potential energy alone.
In this section, it will be demonstrated how to make the right calculation for the total released energy of the reaction and the single energy of each reaction product.
The Deuterium-Tritium fusion from the previous paragraph will be taken as an example.
To calculate the total energy of the products, we must add the net force of the neutron given by Eq. (1a) to the net force of helium-4 given by Eq. (17). The resultant net force of the products is then:
F_{He4-N}=-\frac{4kq^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{4kq^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5}-\frac{kq^2\left(\left(1-\frac{v^2}{c^2}\right)r-\frac{2r^2a}{c^2}\right)}{r^3}+\frac{kq^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}-\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}+\frac{r^4a}{c^2}\right)}{r^5} (25)
Now let’s find the distance between charge centers for the released energy (for v = 0 and a = 0):
-{2.81983\ 10}^{-12}=-\int_{{10}^{27}}^{r}F_{He4-N}dr;
r=0.408\ {10}^{-15}mThen, the total products’ energy from the fusion will be:
E_p=-\int_{{10}^{27}}^{{0.408\ 10}^{-15}}F_{He4-N}drE_p=-2.820392157\times{10}^{-12}-1.497547959\times{10}^{-42}a+3.133769063\times{10}^{-29}v^2 (26)
Where v, a are the relative velocity and acceleration between the particles.
On the other hand, the released energy is the total energy of the reactants minus the total energy of the products (Eq. 24 minus Eq. 26):
E_{rel}=E_r-E_p={2.8198310}^{-12}\ JoulesE_{rel}=-7.355155092\times{10}^{-12}-3.980739327\times{10}^{-42}a+5.039250104\times{10}^{-29}v^2=0 (27)
Where v,\ a are the relative velocity and acceleration between the particles.
Solving the equation system given by Eq. (26) and Eq. (27) gives us the values of the relative velocity and acceleration.
v=\pm\ 6.56\ {10}^7\ \frac{m}{s}, a=-\ 1.79\ {10}^{30}\ \frac{m}{s^2} (27a)
Where v=(v_{He4}-v_N) and a=(a_{He4}-a_N). As we have four unknowns, we need four equations to get the solutions. The four equations will be: E_{rel}, E_p, E_{He4} and E_N.
The total energy of Helium-4 for the released energy is given by the following equation:
E_{He4}=2.256313725\times{10}^{-12}+1.996730613\times{10}^{-42}a-2.507015251\times{10}^{-29}v^2 (28)
The system of Equations
Our system of equations is made up of Eq. (1b), Eq. (26), Eq. (27) and Eq. (28), which are rewritten below in terms of the single velocity and acceleration of the products:
E_{rel}=-7.355155092\times{10}^{-12}-3.980739327\times{10}^{-42}(a_{He4}-a_N)+5.039250104\times{10}^{-29}{(v_{He4}-v_N)}^2=0;
E_p=-2.820392157\times{10}^{-12}-1.497547959\times{10}^{-42}(a_{He4}-a_N)+3.133769063\times{10}^{-29}{(v_{He4}-v_N)}^2;
E_{He4}=2.256313725\times{10}^{-12}+1.996730613\times{10}^{-42}a_{He4}\ -2.507015251\times{10}^{-29}v_{He4}^2;
E_N=-3.408026062\times{10}^{-13}+4.966056036\times{10}^{-43}a_N+3.786695625\times{10}^{-30}v_N^2The four solutions of this system are:
- v_{He4}=-\ 3.635803959\ {10}^7\ \frac{m}{s}; a_{He4}=-1.113406736\ {10}^{30}\ \frac{m}{s^2}; v_N=\ 2.931466029\ {10}^7\ \frac{m}{s}; a_N=6.79681560\ {10}^{29}\ \frac{m}{s^2}
- v_{He4}=-1.32685352\ {10}^7\ \frac{m}{s}; a_{He4}=-1.127793609\ {10}^{30}\ \frac{m}{s^2}; v_N=\ 5.240416466\ {10}^7\ \frac{m}{s}; a_N=6.652946875\ {10}^{29}\ \frac{m}{s^2}
- v_{He4}=3.635803959\ {10}^7\ \frac{m}{s}; a_{He4}=-1.113406736\ {10}^{30}\ \frac{m}{s^2}; v_N=\ -2.931466029\ {10}^7\ \frac{m}{s}; a_N=6.79681560\ {10}^{29}\ \frac{m}{s^2}
- v_{He4}=1.32685352\ {10}^7\ \frac{m}{s}; a_{He4}=-1.127793609\ {10}^{30}\ \frac{m}{s^2}; v_N=\ -5.240416466\ {10}^7\ \frac{m}{s}; a_N=6.652946875\ {10}^{29}\ \frac{m}{s^2}
The velocity of the products in solutions 2) and 4) coincides with the values obtained in the conventional Mechanics calculations in the prior section. The relative velocity and acceleration given in (27a) are also satisfied.
Solution 2) will be taken for the calculation that follows.
Generic Total Energy Equation for Helium-4
The net force for Helium-4 nucleus is given by Eq. (17). Now let’s calculate the generic equation for the total energy:
E_{He4}=-\int_{r_i}^{r_f}{F_{He4}\ dr}Where r_i, r_f are the initial and final distances between charge centers. After integration, we get the generic expression of the total energy of Helium-4:
E_{He4}=-4kq^2\left(\frac{1}{r_f}\right)+\frac{4kq^2}{c^2}\left(\frac{1}{r_f}\right)\cdot v^2+\frac{8kq^2}{c^2}\left(\ln{\left(r_f\right)}-\ln{\left(r_i\right)}\right)\cdot a (29)
As we have seen in the derivation of the total energy in Part 2, the second term is the classic kinetic energy, which is related to the mass and velocity of the particle. From this term, we are going to make a very accurate estimation of the distance between charge centers r_f. Recall from the derivation of the total energy in Part 2 that the mass is given by m_{sys}=\frac{2kq_1q_2}{c^2}\left(\frac{1}{r_f}-\frac{1}{r_i}\right), which in our case turns out to be: m_{He4}=\frac{8\ kq^2}{c^2}\left(\frac{1}{r_f}\right). Therefore, we can write the second term as follows, and solve for r_f:
\frac{4kq^2}{c^2}\left(\frac{1}{r_f}\right)v_{He4}^2=\frac{1}{2}\cdot m_{He4}\cdot v_{He4}^2r_{fHe4}=3.1\ {10}^{-18}m (30)
Recall that the initial distance was chosen to be: r_i={10}^{27}m.
Evaluation of the Total Energy of Helium-4 and the Single Terms that make it up
Taking solution 2) from previous paragraphs, we’ll get the values of the total energy of Helium-4 that is released in the Deuterium-Tritium fusion and evaluate the magnitude of the single terms in the total energy equation.
E_{He4}=-4kq^2\left(\frac{1}{r_{fHe4}}\right)+\frac{4kq^2}{c^2}\left(\frac{1}{r_{fHe4}}\right)\cdot v_{He4}^2+\frac{8kq^2}{c^2}\left(\ln{\left(r_{fHe4}\right)}-\ln{\left(r_i\right)}\right)\cdot a_{He4}=2.965505961\times{10}^{-12}\ JoulesE_{He4}=18.4\ MeV (31)
Now let’s evaluate the single terms of the total energy equation above (Eq. 29):
U_{He4}=-4kq^2\left(\frac{1}{r_{fHe4}}\right)=-9.205760000\times{10}^{-28}\ Joules\ \cong0\ MeV potential energy
K_{He4}=\frac{4kq^2}{c^2}\left(\frac{1}{r_{fHe4}}\right)\cdot v_{He4}^2=5.809000428\times{10}^{-13}\ Joules\ =\ 3.6\ MeV kinetic energy (32)
E_{rad}=\frac{8kq^2}{c^2}\left(\ln{\left(r_{fHe4}\right)}-\ln{\left(r_i\right)}\right)\cdot a_{He4}=2.364486072\times{10}^{-12}\ Joules=14.75\ MeV radiation energy (33)
The Radiation Frequency of the Alpha Particle
We can apply the Planck equation to the result (33) to calculate the radiation frequency, recalling that the Planck constant is h={6.6260701510}^{-34}\ \frac{J}{Hz}.
f=\frac{E_{rad}}{h}=3.56\times{10}^{21}\ HzThis frequency corresponds to gamma radiation.
Generic Total Energy Equation for the Neutron (electron-proton bound)
The net force for the neutron is given by Eq. (1a). Now let’s calculate the generic equation of the total energy:
E_N=-\int_{r_i}^{r_f}{F_N\ dr}Where r_i, r_f are the initial and final distance between charge centers. After integration, we get the generic expression for the total energy of the Neutron:
E_N=-kq^2\left(\frac{1}{r_f}\right)+\frac{kq^2}{c^2}\left(\frac{1}{r_f}\right)v^2-\frac{2kq^2}{c^2}\left(\ln{\left(r_f\right)}-\ln{\left(r_i\right)}\right)\ a (34)
As we have seen in the derivation of the total energy in Part 2, the second term is the classic kinetic energy, which is related to the mass and velocity of the particle. From this term, we are going to make a very accurate estimation of the distance between charge centers r_f. Recall from the derivation of the total energy in Part 2 that the mass is given by m_{sys}=\frac{2kq_1q_2}{c^2}\left(\frac{1}{r_f}-\frac{1}{r_i}\right), which in our case turns out to be: m_N=\frac{2\ kq^2}{c^2}\left(\frac{1}{r_f}\right). Therefore, we can write the second term as follows, and solve for r_f:
\frac{kq^2}{c^2}\left(\frac{1}{r_f}\right)v_N^2=\frac{1}{2}\cdot m_N\cdot v_N^2r_{fN}=3.05\ {10}^{-18}m (35)
Recall that the initial distance was chosen to be: r_i={10}^{27}m.
Evaluation of the Total Energy of the Neutron and the Single Terms that make it up
Taking solution 2) from previous paragraphs, we’ll get the values of the total energy of the Neutron (electron-proton pair) that is released in the Deuterium-Tritium fusion and evaluate the magnitude of the single terms in the total energy equation.
E_N=-kq^2\left(\frac{1}{r_{fN}}\right)+\frac{kq^2}{c^2}\left(\frac{1}{r_{fN}}\right)v_N^2-\frac{2kq^2}{c^2}\left(\ln{\left(r_{fN}\right)}-\ln{\left(r_i\right)}\right)a_N=2.651205890\times{10}^{-12}\ JoulesE_N=16.5\ MeV (36)
Now let’s evaluate the single terms of the total energy equation above (Eq. 34):
U_N=-kq^2\left(\frac{1}{r_{fN}}\right)=-2.301440000\times{10}^{-28}\ Joules\cong0\ MeV potential energy
K_N=\frac{kq^2}{c^2}\left(\frac{1}{r_{fN}}\right)v_N^2=2.302443138\times{10}^{-12}\ Joules\ =14.4\ MeV kinetic energy (37)
E_{rad}=-\frac{2kq^2}{c^2}\left(\ln{\left(r_{fN}\right)}-\ln{\left(r_i\right)}\right)a_N=3.487627523\times{10}^{-13}\ Joules=2.17\ MeV radiation energy (38)
The Radiation Frequency of the Neutron (electron-proton pair)
We can apply the Planck equation to the result (38) to calculate the radiation frequency, recalling that the Planck constant is h={6.6260701510}^{-34}\ \frac{J}{Hz}.
f=\frac{E_{rad}}{h}=5.24\times{10}^{20}\ HzThis frequency corresponds to gamma radiation.
Verifying if the Total Momentum change is satisfied by the solutions
The total momentum change was derived in Part 2, but let’s quickly calculate it for the fusion products. The net forces of Helium-4 and Neutron are:
F_{He4}=-\frac{4kq^2\left(\left(1-\frac{v^2}{c^2}\right)r+\frac{2r^2a}{c^2}\right)}{r^3}+\frac{4kq^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}+\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}-\frac{r^4a}{c^2}\right)}{r^5};
F_N=\left(-\frac{kq^2\left(\left(1-\frac{v^2}{c^2}\right)r-\frac{2r^2a}{c^2}\right)}{r^3}+\frac{kq^2\left(1-\frac{v^2}{c^2}\right)\left(\left(\frac{v^2r^2}{c^2}-\frac{r^3a}{c^2}\right)r-\frac{v^2r^3}{c^2}+\frac{r^4a}{c^2}\right)}{r^5}\right)The momentum change of the products is given by the integral of the forces in time, where r is the distance between charge centers for the released energy (r=0.408\ {10}^{-15}m) and v,a the relative velocity and acceleration.
P_P=\int_{0}^{\frac{r}{v}}\left(F_{He4}+F_N\right)dtAfter integration, we get:
P_P=-\frac{2.820392157\times{10}^{-12}}{v}+3.133769062\times{10}^{-29}v-\frac{1.534293333\times{10}^{-44}a}{v};
P_P=-\frac{2.820392157\times{10}^{-12}}{(v_{He4}-v_N)}+3.133769062\times{10}^{-29}(v_{He4}-v_N)-\frac{1.534293333\times{10}^{-44}(a_{He4}-a_N)}{(v_{He4}-v_N)} (39)
As an example, if we take solution 2) from the “The System of Equations” section above, and plug it in (39), we obtain:
P_p=4.04\times{10}^{-20}=0As P_p\cong0, the momentum change of the products is satisfied.
The Real Released Energy
The energy calculations made for the Deuterium-Tritium fusion products in previous paragraphs, gives us a total released energy that is given by the addition of (31) and (36):
E_{rel}=E_{He4}+E_N=34.9\ MeV.
The scientific community in general ignores the radiation energy and takes it as granted that the released energy is only given by the addition of (32) and (37): K=K_{He4}+K_N=18\ MeV*.
* We have a little difference with the published value of K=17.6\ MeV. This is mainly due to the number of significant figures we used for the calculations.
We see that the real released energy is almost double the kinetic energy of the products.
You can now see how dangerous it is to use incorrect calculation formulas, like the mass defect or excess, which is based on the well-known Einstein equation E=\Delta m\ c^2, and kinetic energy from classical mechanics, which produce insufficient outcomes because they don’t account for radiation.
The mass excess/defect formula can only be used for a quick and accurate calculation of the rest energy (potential energy) of a system of masses. That’s all. The formula doesn’t handle the dynamics of electric charges.
So far as I know, the only equation that will give you the real energy of a system of charges subject to any motion, is the total energy equation that has been derived from the Universal Electrodynamic Force in Part 2.
Conclusions
A method of modifying particle decay rate has been suggested, which may lead to additional possibilities for charge harvesting.
The nuclear structure and total energy calculations have been shown for several nuclei with the derived total energy equation.
It has been demonstrated that the “neutron” is an electron-proton bound in the calculations of energy for some fusions.
The deficient results obtained with usual Classical Mechanics and Einstein’s mass defect/excess calculation have been put into evidence.
The dangers derived from deficient energy calculations have been clearly highlighted.
It has been demonstrated how to calculate the real released energy and the single energy of the products, which includes radiation energy.
It was demonstrated that the real energy amount released in a fusion matched the total energy equation derived from the Universal Electrodynamic Force.
Bibliography
[1]. Raul Fattore, “Negative Mass and Negative Refractive Index in Atom Nuclei – Nuclear Wave Equation – Gravitational and Inertial Control” (2023), Part-1, Part-2, Part-3, Part-4, Part-5, Part-6
[2]. Raul Fattore, “What is Charge? – The Redefinition of Atom – Energy to Matter Conversion” (2023), https://physics-answers.com/what-is-charge-the-redefinition-of-atom-energy-to-matter-conversion/
[3]. David L. Bergman, “Shape & Size of Electron, Proton & Neutron” (2004), Foundations of Science
[4]. N. Graneau, T. Phipps Jr, and D. Roscoe, “An experimental confirmation of longitudinal electrodynamic forces” (2001), The European Physical Journal, https://www.researchgate.net/publication/225353333_An_experimental_confirmation_of_longitudinal_electrodynamic_forces
[5]. V. Milián-Sánchez, F. Scholkmann, et al., “Fluctuations in measured radioactive decay rates inside a modified Faraday cage: Correlations with space weather” (2020), Nature, https://www.nature.com/articles/s41598-020-64497-0
[6]. J.M. Mack, et al., “Remarks on detecting high-energy deuterium–tritium fusion gamma rays using a gas Cherenkov detector” (2006), Los Alamos National Laboratory, Lawrence Livermore National Laboratory, https://www.sciencedirect.com/science/article/abs/pii/S0969806X05003683
[7]. G.R. Mackenzie, et al., “A diamond gammavoltaic cell utilizing surface conductivity and its response to different photon interaction mechanisms” (2021), School of Physics, University of Bristol, https://www.sciencedirect.com/science/article/abs/pii/S2468606921000538
[8]. M. G. Spencer, T. Alam, “High power direct energy conversion by nuclear batteries” (2019), Applied Physics Reviews. 6. 031305. 10.1063/1.5123163, https://www.researchgate.net/publication/335809562_High_power_direct_energy_conversion_by_nuclear_batteries
[9]. K. Hashizume, et al., “Direct Energy Conversion from Gamma Ray to Electricity Using Silicon Semiconductor Cells” (2010), MRS Online Proceeding Library Archive. 1264. 1264-BB05. 10.1557/PROC-1264-BB05-01, https://www.researchgate.net/publication/330650579_Direct_Energy_Conversion_From_Gamma_Ray_to_Electricity_Using_Silicon_Semiconductor_Cells
[10]. Nie Luo, et al., “Proton bremsstrahlung and its radiation effects in fusion reactors” (2010), Department of Nuclear, Plasma and Radiological Engineeing, Univerisity of Illinois, https://www.sciencedirect.com/science/article/abs/pii/S0920379609002440
[11]. INTERNATIONAL ATOMIC ENERGY AGENCY, Fusion Physics, Non-serial Publications, IAEA, Vienna (2012), https://www.iaea.org/publications/8879/fusion-physics
Related articles:
Nuclear Fusion Enhanced by Negative Mass – A Proposed Method and Device – (Part 1)
Nuclear Fusion Enhanced by Negative Mass – A Proposed Method and Device – (Part 2)
Nuclear Fusion Enhanced by Negative Mass – A Proposed Method and Device – (Part 4)
What is Charge? – The Redefinition of Atom – Energy to Matter Conversion
Charge Radiation Derived from the Universal Electrodynamic Force – Proof of the Cherenkov Effect
Faster-Than-Light Travel Feasible with Negative Mass – Superluminal Dynamics
New Atomic Model with Real-Valued Wave Function – Energy Levels, Spectrum, and Atomic Fine Structure
