Raul Fattore
January 27, 2025
Table of Contents
Summary
The study reveals that the electromagnetic wave propagation from a rotating source does not follow a straight line, but the Archimedes spiral trajectory, indicating that most astronomical distance calculations may be incorrect. The research suggests that galaxies are closer to us than previously estimated, potentially indicating a younger universe. The difference between the Archimedes spiral arc length and straight-line estimates is small within our solar system but becomes more significant from Pluto. It is recommended to review all astronomical and cosmological distance and age data.
Acronyms, Abbreviations, Keywords
EMW: electromagnetic wave
EMR: electromagnetic radiation
COMU: center of mass of the universe
Abstract
Since astronomical distance measurements are wrong, this work ought to serve as a possible cautionary tale for all astronomy and cosmology colleagues, as well as for astrophysicists in general.
If this study happens to be validated experimentally, which I’m confident it will be, the implications could be of such a magnitude that it will demand a great part of astronomy and cosmology to be rewritten. Unfortunately, this is not pleasant news.
The problem arose, perhaps due to the poor scientific observation of what Mother Nature shows us and how it works, that resulted in a huge, misdirected effort over many years.
Distance measurement of astronomical objects outside our solar system has been improved step by step through the years each time we wanted to reach more distant objects. This measurement improvement took the form of what we know as the “cosmic distance ladder.”
Every cosmic ladder technique performs best within a specific range of distances. But they are all impacted by what could be a significant flaw. This study shows the cause of the potential flaw as well as how to measure astronomical distances in a more realistic way.
- Does light follow a rectilinear path?
- Are distance measurement methods of the “cosmic distance ladder” providing the right results?
- Are galaxies really receding?
- Do receding galaxies mean that the universe is expanding?
- Can we better determine the age of the universe?
- Could galaxies collide?
All these questions are answered in the development of this study according to the suggested theories.
Introduction
The fact that astronomical distances are wrong demands some thoughts on important matters about our universe.
As stated in the article “Dynamic Deformation of Earth and Motion Effects Caused by Universe’s Gravitational Field” [1], the states of “rest” and “rectilinear” motion do not exist in the universe.
Accelerated motion is present in all cosmic objects in the universe. The simultaneous existence of translational and rotational motion is evident everywhere in the cosmos.
This is true for groups of celestial objects like galaxy clusters, solar systems, and galaxies. Centripetal acceleration is the secondary cause of acceleration, whereas gravitational force is the primary reason.
Evidence that all cosmic objects spin around the COMU is still lacking. But if we use logic, we may deduce that they do. The COMU may be the starting point of everything, akin to the “Master Black Hole” or something else we don’t yet understand.
The idea of “receding galaxies” will be invalidated if everything revolves around the COMU. Galaxy clusters will have “priority” over less massive objects in finding stable orbits around the COMU because of their mass magnitude. This suggests that they will organize according to the quantized Titius-Bode law.
Assuming that these objects are in stable orbits, it is natural that the relative velocity among them will increase or decrease within a certain range. This does not necessarily mean that galaxies are receding or eventually coming in our direction for a collision.
If all cosmic objects rotate around the COMU, then the theory of the “universe expansion” will also become invalid.
In this case, time is the problem. It might take humankind many millions of years to monitor and document the changes in order to verify this.
The study about “Full Free Motion of Celestial Bodies Around a Central Mass – Why Do They Mostly Orbit in the Equatorial Plane?” [2] is an exhaustive investigation about the orbit and position of a small mass around a much bigger one. There is a scheme of position of the orbiting mass that could eventually be extrapolated to much more massive objects. We see there that masses near the main one may adopt any position around.
If there are single galaxies in that region (near the COMU), there is a significant chance that they will collide before they can eventually settle into a stable position.
Nowadays, we know that gravity is an EMW of atomic origin caused by dipole oscillation in the atom [3] [4]. So, gravitational waves are electromagnetic waves, and space is not something mechanical that can be moved. You cannot grant geometrical properties to a force of electromagnetic origin. There is no such thing as “ripples in space-time”, as proposed by the ill-fated theory of Einstein.
When a cosmic object explodes or collapses, a gravitational electromagnetic shock wave pulse of immense amplitude is generated, which modulates the tail or final part of the regular wave. Cosmic explosions carry out colossal amounts of electromagnetic energy in the form of momentum.
This huge momentum pulse will shake all cosmic objects. Then, it is absolutely natural to expect a mechanical vibration and even a push on them.
That’s the reason we have an extremely sensitive interferometer on Earth that can detect the tail pulse of gravitational electromagnetic waves from cosmic cataclysms. It detects the Earth vibration caused by the momentum of the pulse, not the “ripples in space-time”. Still, highly sensitive seismic instruments might also identify even more massive cosmic explosions.
Following that, we will examine how to use the well-known law of “rectilinear propagation of light” to determine cosmic distances in the absence of medium change or obstructions. This will prove that astronomical distance measurements are wrong.
The Real Path of Light Needed for Astronomical Distance Measurements
You may get an idea of what’s happening immediately from the example that follows.
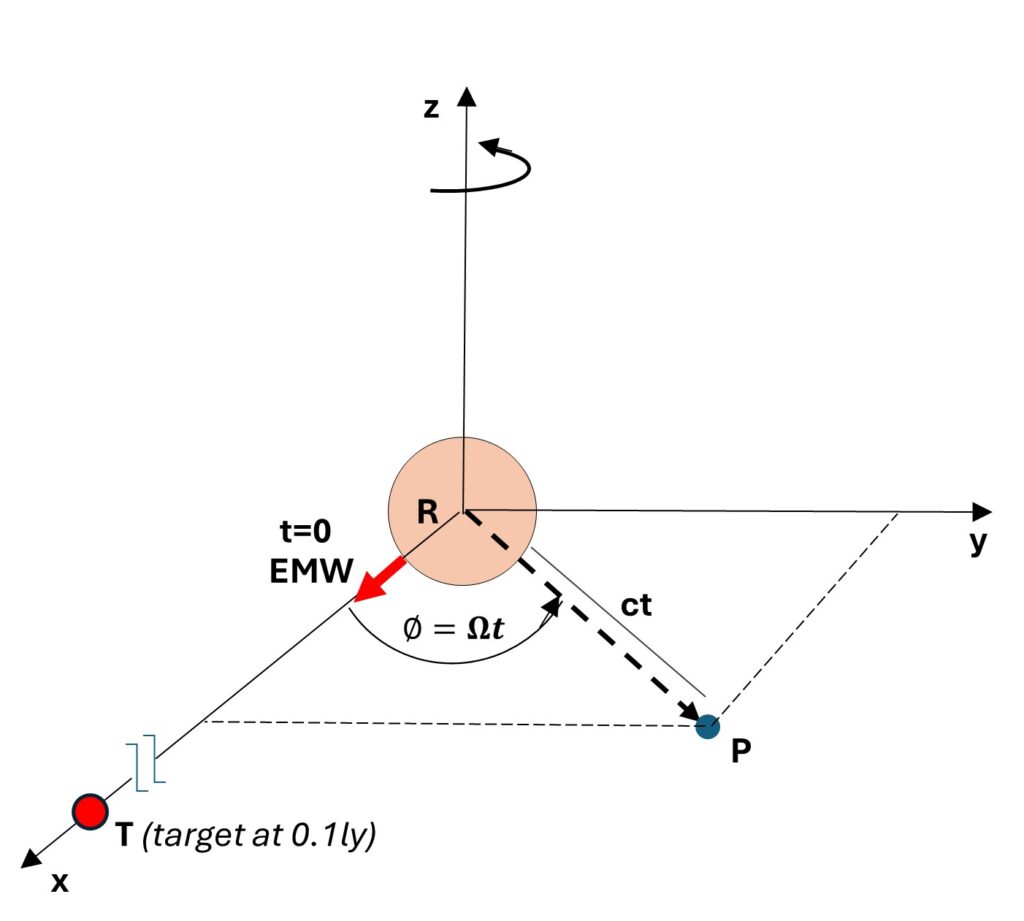
Sending an electromagnetic wave to target T at 0.1ly
In Fig. 1 we have Earth at the origin of the coordinates. The plane x-y intersects Earth at the equator, while the z-axis is the rotational axis of our planet.
Assume that we want to send a message to target T, which we know is exactly at a linear distance of 0.1ly in the direction of the x-axis.
From a location on the equator, we point our wave source in the direction of the target T and send an EMW at t=0.
For simplicity, we’ll ignore atmospheric refraction and assume a rectilinear propagation of the EMW at constant velocity c.
Let P be a central point of the wavefront lying on the x-y plane. At a time t, point P covered a distance ct, while Earth rotated an angle \emptyset=\Omega t. The coordinates of point P on the wavefront are:
x=\left(R+ct\right)\ \cos{\left(\Omega t\right)} (1)
y=\left(R+ct\right)\ \sin{\left(\Omega t\right)} (2)
z=0Equations (1) and (2) are the parametric equations of the Archimedes spiral, where R=6.378\ {10}^6[m] is the Earth radius, c=3\ {10}^8[\frac{m}{s}] is the speed of light, and \Omega=7.29\ {10}^{-5}[\frac{r}{s}] is the angular velocity of Earth’s rotation.
The real wavefront path will travel a greater distance to target T because point P will follow a spiral trajectory rather than a straight line.
As we know the linear distance to the target T, the time taken for the EMW to cover that linear distance is t=\frac{0.1ly}{c}=3.153666667\ {10}^6[s].
Replacing this time in Eq. (1) and (2), we obtain the coordinates and magnitude of vector \vec{r}:
The real path length of the EMW is given by the arc length of the Archimedes spiral:
L =\int_{0}^{t}{||\dot{\vec{r}}||}dt (3)
When solving integral (3) for the time required in the linear distance, we get:
L =\int_{0}^{3.153666667\ 10^6}{||\dot{\vec{r}}||}dt = 1.087689280\ 10^{17} [m] = \bf 11.49 [ly]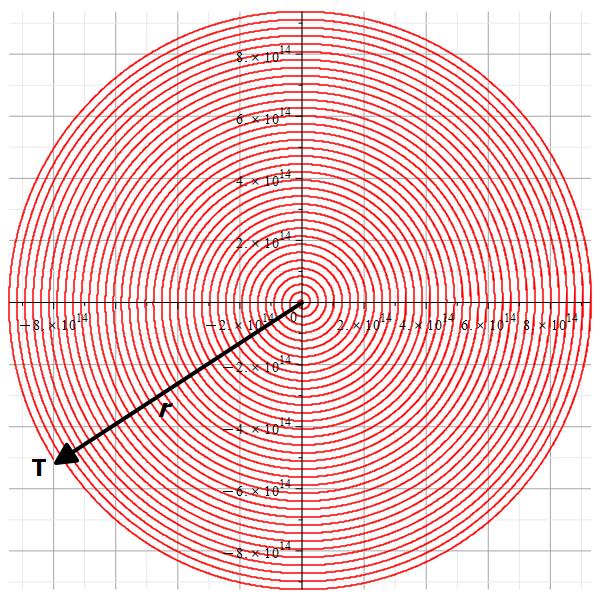
The spiral path of the electromagnetic wave and the position vector showing the linear path
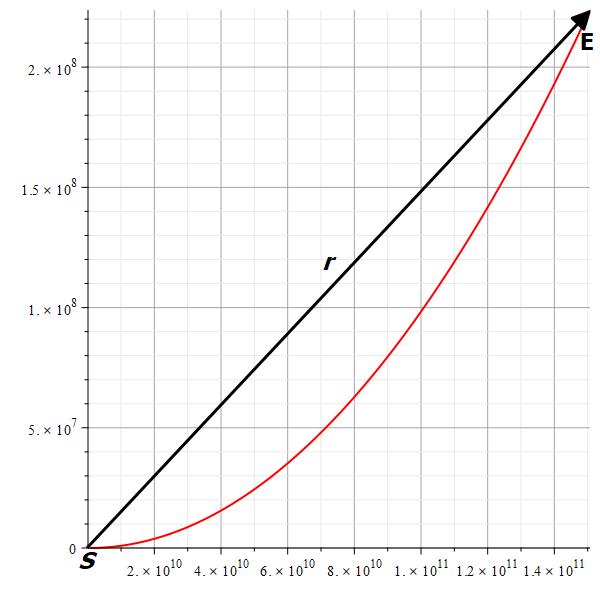
Figure 2 shows a graph of the linear, straight path to target T given by ||\vec{r}|| and the real path traveled by the EMW until reaching target T at the end of the Archimedes spiral, which is given by the arc length.
The distance ratios between the paths are:
We may observe that the two distances differ significantly from one another.
The straight distance is just ~0.87% of the real light path, or ~115 times shorter!
If someone in the target T takes astronomical distance measurements of our EMW, he or she will believe that we are located 11.49\ [ly] away.
Can you perceive what’s going on now?
This demonstrates that astronomical distance measurements are wrong without depending on Einstein’s incorrect theory of relativity, which cannot account for the true behavior of Mother Nature.
Since this fact will fundamentally alter not only the vast amount of data but also some of the notions of astronomy and cosmology as we currently understand them, I’m quite worried about the huge impact and consequences that this fact will have on these fields.
Let’s take a deep breath and then move on to a few scenarios of distance calculations both inside and outside our solar system.
Some remarks about the Archimedes spiral’s uses in astronomical distance measurements
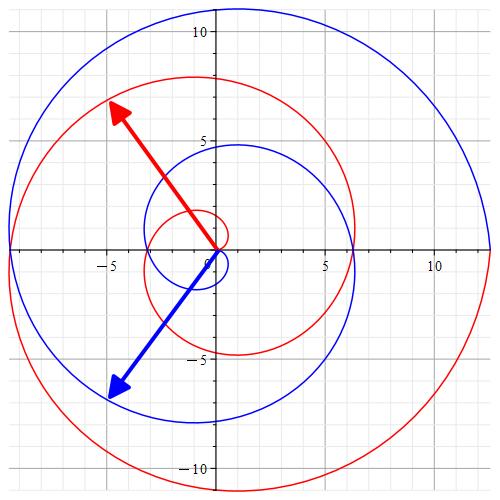
Specular property of the Archimedes spiral
Specular property of the Archimedes spiral
As shown in Fig.2a the spiral is specular with respect to the x-axis depending on the rotation direction.
The figure shows two spirals. The red one, which rotates counterclockwise, and the blue one, which rotates clockwise.
The same position vector example is shown for both spirals.
Note that the position vectors will have opposite y-coordinates.
The Archimedes spiral for constant angular acceleration in astronomical distance measurements
The cosmic objects considered in the EMW transmission examples in this work are assumed to rotate at a constant angular velocity (zero angular acceleration). This appears to be true for every cosmic object that we have seen thus far.
Now imagine that there are some celestial objects that generate electromagnetic waves while spinning with a constant angular acceleration. We will refer to the resulting Archimedes spiral as a “accelerated Archimedean spiral” and compare it to the standard spiral for the same time interval in Figs. 2b and 2c.
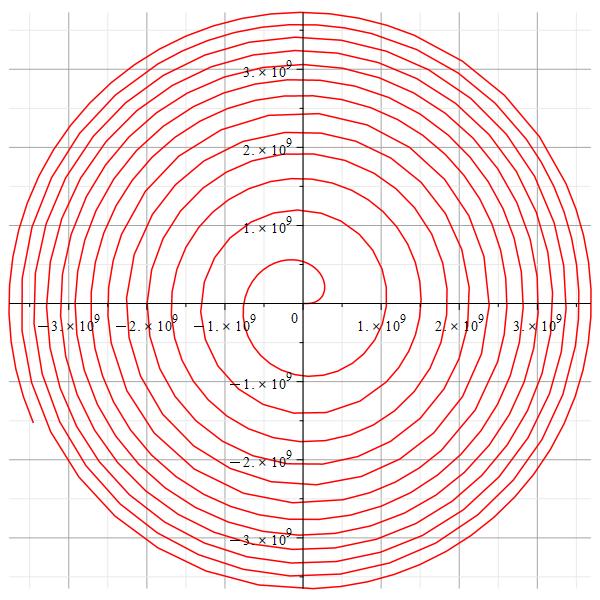
The Archimedes spiral for constant angular acceleration
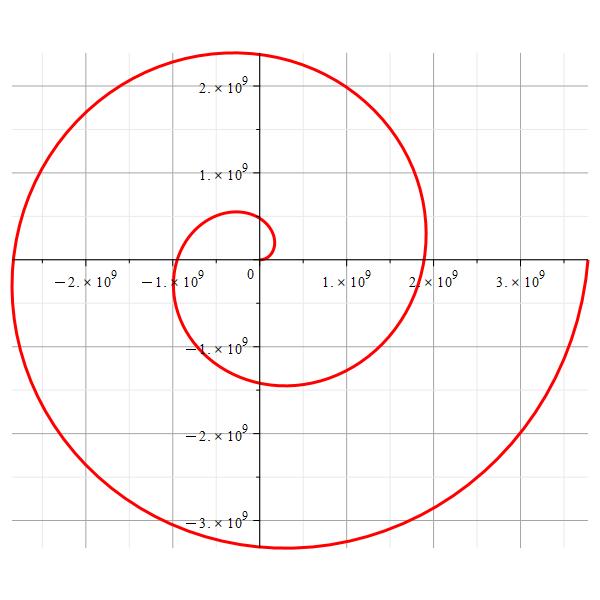
The regular Archimedes spiral
We can observe a notable length difference for the same interval. Let’s name the arc length of Fig. 2b as L_b, and the arc length of Fig. 2c as L_c. In Figs. 2d and 2e is shown the linear relationship between the arc length difference \Delta L= L_b-L_c and time.
During the first few seconds, L_c>L_b. Then starts to be in favor of L_b until reaching a time where huge differences start to appear, that is, L_b\gg\ L_c.
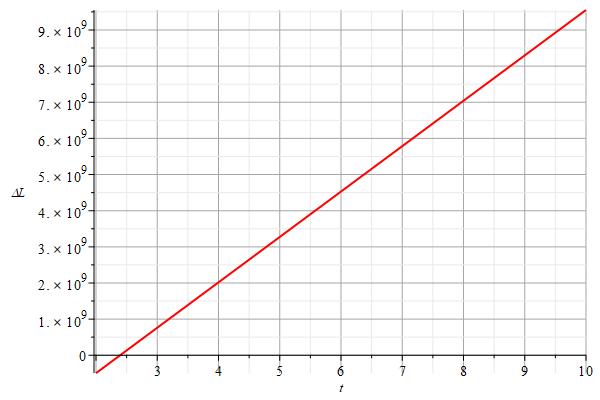
The difference in distance within a few seconds after the EMW was emitted
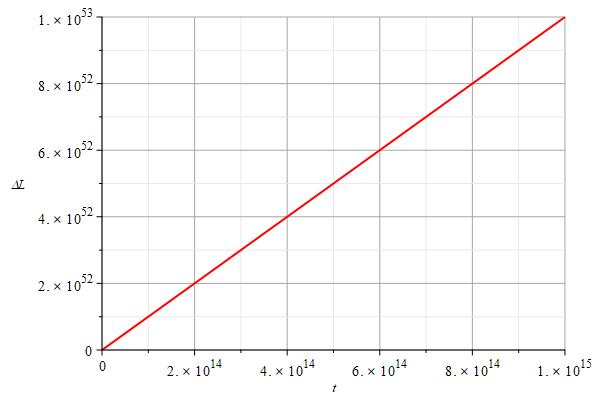
The difference in distance for a longer time after the EMW was emitted
The emitted EMW will take a much longer time for a given distance if a celestial object happens to spin with constant angular acceleration as opposed to constant angular velocity.
We stated that astronomical distance measurements are wrong; however, in this case they will be worse.
The spatial Archimedean spiral becomes a straight line in the limit
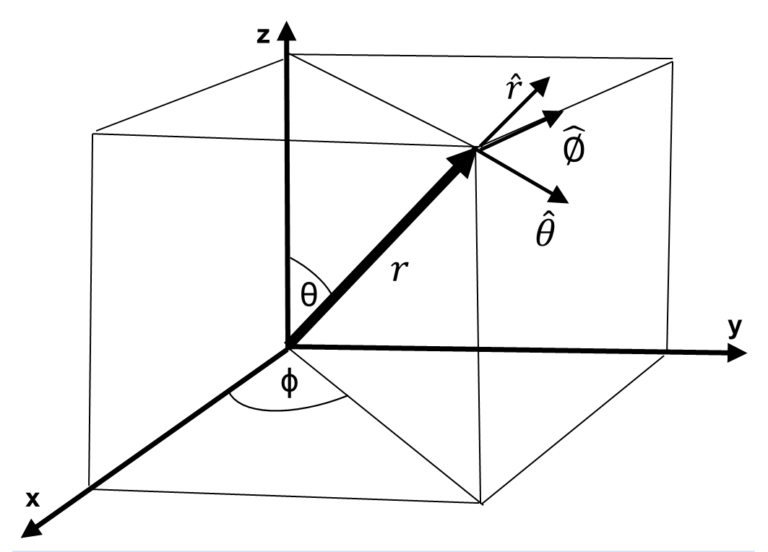
Convention in spherical coordinates
+θ when measured clockwise from +z
+ϕ when measured counterclockwise from +x
+r when measured outwards from the origin
The parametric spatial equations of the Archimedes spiral in spherical coordinates are:
Astronomical distance measurements are wrong in general. In the previous section, we transmitted the EMW from the equatorial plane, as shown in Fig. 1. In this case the Archimedes spiral is planar (2D space), and it is located on the plane x-y, as shown in Fig. 2g.
When the EMW is radially emitted from other latitudes different from the equator, the spiral path will evolve in a volume of space (3D space). In this case, the path length of the emitted EMW will depend on the latitude of the EMW emitter, as shown in Figs. 2h and 2i.
There exists an ideal condition of transmission of the EMW where the spiral trajectory could almost be suppressed and the path length is minimum, as shown in Fig. 2i. This is the case when the EMW is radially emitted along the rotational axis of the celestial object (\theta=0\ or\ \pi).
In the example given in Fig. 1, for \theta=\frac{\pi}{4} we get L=7.691988567\times{10}^{16}m=\bf 8.13\left[ly\right], while for \theta=\frac{\pi}{9} we get L=3.722993486\times{10}^{16}m=\bf 3.93\left[ly\right]. Distance differences are notable.
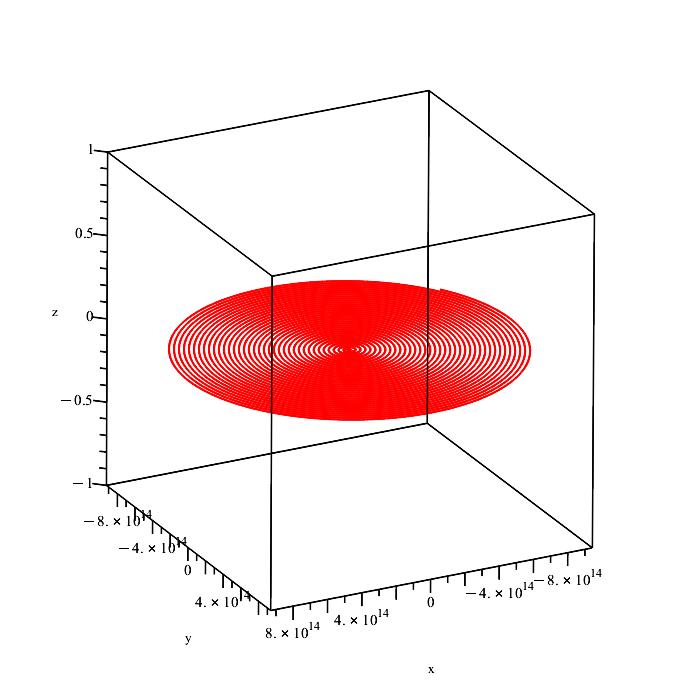
The planar spiral path of the electromagnetic wave radially transmitted from the equator
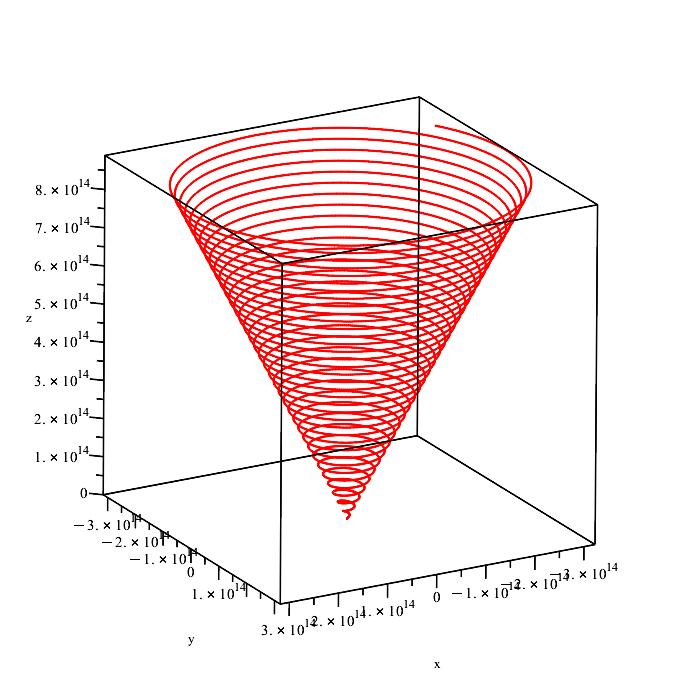
The 3D spiral path of the electromagnetic wave radially transmitted from a latitude different from the equator
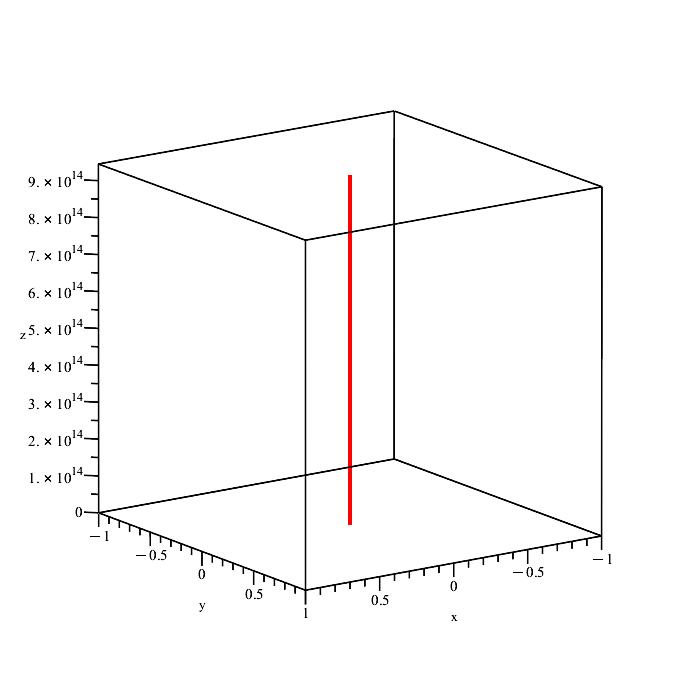
The ideal rectilinear path of the electromagnetic wave radially transmitted along the Earth’s rotational axis
As astronomical distance measurements are wrong, we need to find a way to minimize the error in the calculations. We know a star emits EMW in all directions. What latitude of the star should we take for the measurement?
This fact might only be taken into account for distance measurements of cosmic objects located within a range of “short” cosmic distance.
The masses that orbit distant stars in the equatorial plane can be used to estimate the direction of the star’s rotational axis and calculate the axis’ relative inclination with respect to us.
With this information, we may estimate an approximate star’s latitude from which we are receiving light with the shortest possible path and determine the most approximate distance.
We can only estimate the two extreme distance values—the minimum route of the light path coming from the observed cosmic object’s rotational axis and the maximum path of light estimated from its equatorial plane—if we are unable to determine the direction of the object’s rotational axis. In this approach, an approximate average might be made.
For very distant cosmic objects, the difference between maximum and minimum distance could be so tiny compared to their distance to us that we might be tempted to ignore it, yielding thus to huge distance errors.
The real light path between the Sun and Earth
In general, astronomical distance measurements are wrong. Fortunately, the difference between the measured values and the real straight distances is tiny within our solar system.
For this calculation we are going to take the sun’s radius and rotational angular velocity data from its equator, as well as the estimated distance to Earth as follows:
We can now calculate the time needed for light to cover the path Sun-Earth by calculating the arc length of the Archimedes spiral from Eq. (1) and (2).
L =\int_{0}^{t}{||\dot{\vec{r}}||}dt = 150\ 10^{9} [m]After solving the integral, we obtain t=499.9998136\ [s]. Now we can calculate the coordinates for Earth and the straight distance given by ||\vec{r}||.
The spiral path of the light between sun and earth
Figure 3 shows a graph of the linear, straight path from Sun (S) to Earth (E) given by ||\vec{r}|| and the real path traveled by the light until reaching Earth at the end of the Archimedes spiral, which is given by the arc length.
The distance ratios between the paths are:
We see that there is no significant difference between the distances. The straight distance is just ~0.46% longer or 0.995 times the light path.
Note: The spiral curve should be longer than the rectilinear distance, so the error could be due to some wrong estimation of the sun parameters or distance sun-earth.
The real light path between the Sun and Pluto
For this calculation we are going to take the sun’s radius and rotational angular velocity data from its equator, as well as the estimated distance to Pluto as follows:
We can now calculate the time needed for light to cover the path Sun-Pluto by calculating the arc length of the Archimedes spiral from Eq. (1) and (2).
L =\int_{0}^{t}{||\dot{\vec{r}}||}dt = 6\ 10^{12} [m]After solving the integral, we obtain t=19988.26161[s]. Now we can calculate the coordinates for Pluto and the straight distance given by ||\vec{r}||.
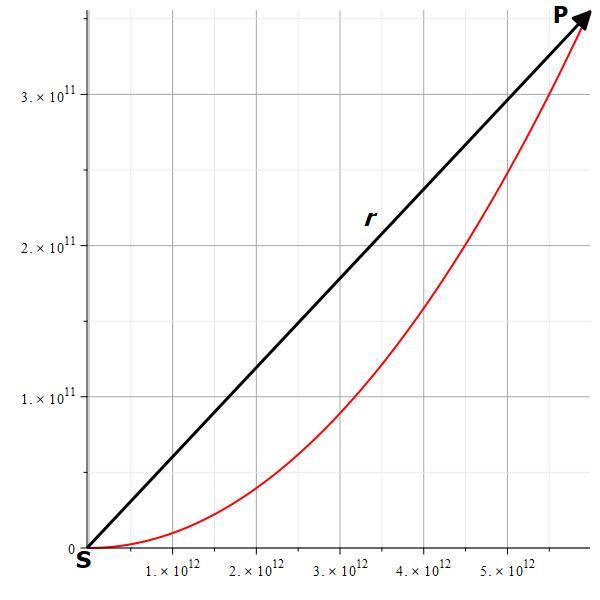
The spiral path of the light between the sun and Pluto
Figure 4 shows a graph of the linear, straight path from Sun (S) to Pluto (P) given by ||\vec{r}|| and the real path traveled by the light until reaching Pluto at the end of the Archimedes spiral, which is given by the arc length.
The distance ratios between the paths are:
We may observe that astronomical distance measurements do not significantly differ from one another. The straight distance is just around 0.05%, or about 0.999 times, shorter than the light path.
The real path of the signal between Earth and the Voyager-1 probe –within astronomical distance measurements
As astronomical distance measurements are wrong, this case is within a distance range that deserves attention.
For this calculation we are going to take the following data for Earth, as well as an estimated distance to Voyager-1 in present time as below:
We can now calculate the time needed for the signal to cover the path Earth-Voyager 1 by calculating the arc length of the Archimedes spiral from Eq. (1) and (2).
L =\int_{0}^{t}{||\dot{\vec{r}}||}dt = 2.49\ 10^{13} [m][After solving the integral, we obtain two different solutions, t=42849.63916[s] and t=-50640.08741[s]. By taking the positive solution, we can now calculate the coordinates for Voyager-1 and the straight distance given by ||\vec{r}||.
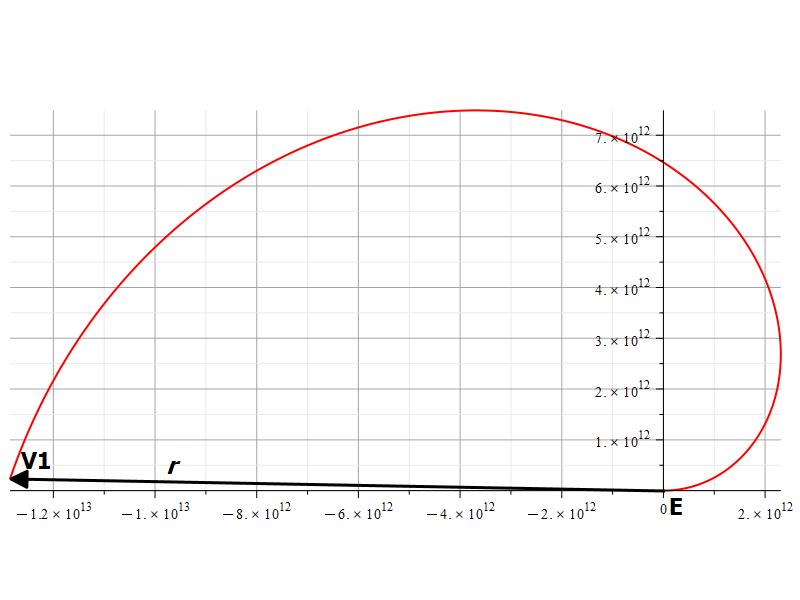
Spiral path of electromagnetic wave from Earth to Voyager 1 probe
Figure 5 shows a graph of the linear, straight path from Earth (E) to Voyager-1 (V1) given by ||\vec{r}|| and the real path traveled by the signal until reaching Voyager-1 at the end of the Archimedes spiral, which is given by the arc length.
The distance ratios between the paths are:
The disparity in the distances is evidently substantial. The signal path is around 1.94 times longer than the straight distance, which is about 52% shorter!
We noted that astronomical distance measurements are wrong, and this fact becomes of importance from certain distance ranges.
If Voyager-1 does not spin and is continuously pointing its antenna to Earth, the signal it sends to us may follow an approximate rectilinear path. We should take this fact into account when calculating distances in both directions.
The Arecibo message – The reply message could not be fake
This is a sensitive case intimately linked to the fact that astronomical distance measurements are wrong.
In 1974, we used the radio telescope in Arecibo to transmit a message into space as part of humankind’s attempt to communicate with other intelligent civilizations. The target of the communication was M13’s present position, which is roughly 25,000 light years away from Earth.
In 2001, 27 years later, we got a response—not in the form of an EMW, but as a printed message on a crop—using extremely precise, highly advanced EMR technology—a technique we do not yet have. The response was seen as fraudulent and ascribed to a potential crop artist. This response was recorded in Hampshire, UK, close to the Chilbolton radio telescope.
Only narrow-minded, conceited, and petty human brains can believe that the only planet in the cosmos with both intelligent and non-intelligent species is Earth. We send messages in the hope of receiving a response. And we reject the response when it arrives?
The quickness of the response was the primary factor in why it was deemed fraudulent.
Even if it sounds absurd, some astronomers only anticipate hearing back from M13—that is, in 50,000 years. In addition to ignoring the beam divergence that always occurs, even in highly collimated beams, which is a feature that will enable reaching other cosmic objects “out of path,” they always consider an unhindered path for the wave.
As the answer took 27 years, we may assume that our message was received in 13.5 years and replied to immediately, so that the receiver civilization is to be found at a distance of 13.5\ \left[ly\right]=\ 1.2772\ {10}^{17}\ [m].
We are going to take the following data for Earth, as well as the estimated distance to the receiver civilization as below:
As we already know from previous paragraphs, this distance is the path taken by the answer, which is given by the Archimedes spiral arc length.
L =\int_{0}^{t}{||\dot{\vec{r}}||}dt = 1.2772\ 10^{17} [m]When solving the integral, we get t=3.417406016\ {10}^6\ [s]. Now we can calculate the coordinates for the receiver civilization and the straight distance given by ||\vec{r}||.
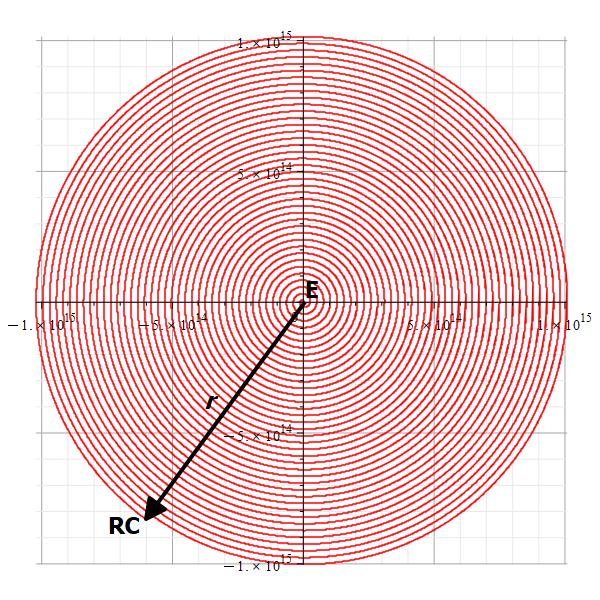
Spiral path of the Arecibo message from Earth to the receiver civilization
Figure 6 shows a graph of the linear, straight path from Earth (E) to the receiver civilization (RC) given by ||\vec{r}|| and the real path traveled by the signal until reaching the RC at the end of the Archimedes spiral, which is given by the arc length. This can be another proof that astronomical distance measurements are wrong.
The distance ratios between the paths are:
We can observe that the distances differ by a fairly large amount. The straight distance is approximately 124.5 times shorter than the signal path, or ~0.8% shorter!
There are several cosmic objects within the range of 13.1\ [ly] and 13.8\ [ly] as: Kruger 60A, Kruger 60B, DEN J1048-3956, Ross 614 A, Ross 614 B and Wolf 1061.
But since the recipient civilization’s message was printed on a crop using extremely precise and sophisticated radiation printing technology, I am convinced that they also possess the ability and/or the technique to send messages that will take the shortest possible trajectory to the target.
They are only 0.11\ [ly] away from us if this is the case. What celestial bodies are situated at this distance? Well, the Oort belt is located thus far from Earth. We can tell that our neighbors might be just around the corner.
Can we send an EMW that propagates in a straight-line trajectory?
The answer is a resounding no.
The fact that astronomical distance measurements are wrong reflects in our own cosmic communications and makes us wonder if we can find some means to overcome or at least minimize the cause.
We may have some ways to minimize the spiral trajectory of an EMW when transmitting from Earth or near it with a satellite but never suppress it because, besides wobbling, we are moving around the sun, while the solar system moves around the center of mass of the Milky Way, which in turn moves around the COMU.
To minimize the Earth’s rotation effect that causes the spiral trajectory of a transmitted EMW, I think of the following options:
- Move the EMW source until reaching a constant velocity equal to and opposite to that of the corresponding Earth latitude. Then send the EMW.
- Place the antenna on the Earth’s rotational axis, whether on the ground or on a satellite, and transmit in the direction of the Earth’s rotational axis. The catch here is that we can only reach cosmic objects in that direction. Any transmission that is off-axis will follow a spiral trajectory, so the beam must be highly collimated to minimize that propagation path.
It is clear that option 1 cannot be accomplished. Until someone else finds more potential answers that I am now unable to figure out, option 2) is a possible alternative.
Conclusions
It was demonstrated that the EMW propagation from a rotating source does not follow a straight line, but the trajectory given by the Archimedes spiral.
As a result, it is evident that the majority of astronomical distance calculations may be wrong.
This research indicates that galaxies are significantly closer to us than previously estimated distances.
Given that distances are shorter than estimated, the universe could be much younger than we now know.
It has been demonstrated that, within our solar system, the difference between the Archimedes spiral arc length and the straight-line estimate is small.
From Pluto onward, these distance difference calculations become more significant.
Although highly unpleasant, it is strongly recommended that all astronomical and cosmological distance and age data be reviewed.
Bibliography
[1]. Raul Fattore, “Dynamic Deformation of Earth and Motion Effects Caused by Universe’s Gravitational Field” (2022), https://physics-answers.com/dynamic-deformation-of-earth-and-motion-effects-caused-by-universe-gravitational-field/
[2]. Raul Fattore, “Full Free Motion of Celestial Bodies Around a Central Mass – Why Do They Mostly Orbit in the Equatorial Plane?” (2022), https://physics-answers.com/full-free-motion-of-celestial-bodies-around-a-central-mass/
[3]. Charles W. Lucas, Jr., “The Electrodynamic Origin of the Force of Gravity” (2008-2009), Part-1, Part-2, Part-3
[4]. A. K. T. Assis, “Gravitation as a Fourth Order Electromagnetic Effect”, Advanced Electromagnetism: Foundations, Theory and Applications, T. W. Barrett and D. M. Grimes (eds.), (World Scientific, Singapore, 1995). https://www.ifi.unicamp.br/~assis/gravitation-4th-order-p314-331(1995).pdf
[5]. M. Martinelli et al, “Forecast constraints on the cosmic distance duality relation with complementary external probes” (2020), https://www.aanda.org/articles/aa/pdf/2020/12/aa39078-20.pdf
[6]. Erika L. Wagoner et al, “Measuring cosmological distances using cluster edges as a standard ruler” (2020), https://academic.oup.com/mnras/article-pdf/504/2/1619/37412612/stab1012.pdf
[7]. Erik D. Reese et al, “Determining the Cosmic Distance Scale from Interferometric Measurements of the Sunyaev-Zeldovich Effect” (2002), https://iopscience.iop.org/article/10.1086/344137/fulltext/
[8]. G. P. Di Benedetto, “Towards a fundamental calibration of the cosmic distance scale by Cepheid variable stars” (2013), https://academic.oup.com/mnras/article-pdf/430/1/546/3087489/sts655.pdf
Related articles:
Dynamic Deformation of Earth and Motion Effects Caused by Universe’s Gravitational Field
